1.1 - Analógico y digital
¿Por qué digital? Esta es sin duda la primera pregunta que cualquier lector que está "llegando ahora", y sólo tiene alguna base teórica de la Electrónica, principalmente de la electrónica analógica, como la que se enseña en los primeros volúmenes de esta serie, lo haría cuando encontremos nuestro curso.
Por esta razón, comenzamos nuestro curso precisamente explicando las diferencias entre los dos aparatos electrónicos, para que sean muy claros. Hay que recordar que, en muchos equipos, incluso clasificados como analógicos o digitales, se encuentran los dos tipos de circuitos. Es el caso de ordenadores, procesadores, equipos de telecomunicaciones, automatismos e instrumentos de laboratorio, y muchos otros que, incluso siendo clasificados como "máquinas estrictamente digitales", pueden tener en algunos puntos de sus circuitos ajustes analógicos.
Una definición encontrada en libros especializados asigna el nombre "Electrónica Digital" a los circuitos que operan con cantidades que sólo pueden incrementarse o disminuirse en pasos finitos.
Un ejemplo de esto se da por los circuitos que operan con impulsos. Sólo podemos tener un número entero de pulsos trabajando en cualquier momento en cualquier punto del circuito. En ninguna parte encontramos "medio pulso" o "un cuarto de pulso".
La palabra digital también está asociada con el dígito (del latín digitus de "dedo") que es asociado a la representación de cantidades enteras. No podemos usar nuestros dedos para representar un medio pulso o un cuarto de pulso.
En la electrónica analógica trabajamos con cantidades o señales que pueden tener valores que varían de manera continua en una escala. Los valores de las señales no necesitan ser enteros. Por ejemplo, una señal de audio, que es analógica, varía suavemente entre dos extremos mientras que una señal digital sólo puede variar en saltos, como se muestra en la figura 1.
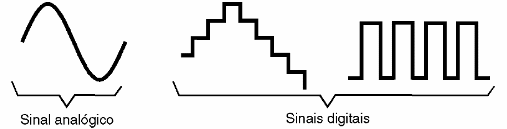
Como el lector puede percibir, la diferencia básica entre los dos tipos de electrónica se asocia inicialmente al tipo de señal con la que trabajan y lo que hacen con las señales.
De una manera resumida hay que decir que:
La electrónica digital funciona con señales que sólo pueden tomar valores discretos o enteros.
La electrónica analógica funciona con señales que pueden tener cualquier valor entre dos límites.
Donde Encontramos La Electrónica Digital
COMPUTADORAS - los ordenadores actuales son digitales en su totalidad, y prácticamente no se utiliza ningún otro tipo de configuración, excepto en la Interconexión con el mundo exterior, porque somos analógicos. Sin embargo, no siempre fue así. En las primeras décadas de este siglo, cuando los circuitos todavía eran usaban válvulas las primeras computadoras eran máquinas analógicas. El imprecisión, y algunas otras dificultades técnicas, que estos ordenadores presentaban hicieron con que ellos se sustituirían por los circuitos digitales que usamos hoy en día.
TELECOMUNICACIONES - Antes también, todos los equipos de las telecomunicaciones trabajaban directamente con las señales analógicas de los micrófonos, de las cámaras de la TV y de otras fuentes. Sin embargo, actualmente la mayoría de las transmisiones de información inalámbrica, por ondas de radio, y por medios físicos tales como fibras ópticas y cables, ocurre en la forma digital. Las señales analógicas se convierten en digitales y por lo tanto se transmiten de una manera mucho más eficiente.
INDUSTRIA Y AUTOMATIZACIÓN - En el pasado, los controles de las máquinas industriales eran simples, sin cambiar de interruptores y llaves o, en lo máximo, dispositivos que controlaban directamente las señales analógicas. También en este caso, hemos tenido una evolución con el uso de microprocesadores, microcontroladores y DSPS (Digital Signal Processors o Procesadores Digitales de Señales). En ellos, las señales analógicas de los sensores y el control se convierten en señales digitales y se utilizan en los equipamientos.
INSTRUMENTACIÓN – La mayoría de los instrumentos de laboratorio son digitales. Con mayor precisión y la capacidad de procesar las medidas que ha realizado, todavía pueden permitirse el lujo de registrar o enviar datos a través de Internet u otros medios de transmisión, con recursos mucho más grandes que los equivalentes analógicos.
ELECTRÓNICA DE CONSUMO – Muchos de los productos electrónicos que usamos hoy en día tienen chips de control que no son más que microcontroladores, que operan de forma totalmente digital. Esto ocurre con su calentador de gas, su horno de microondas, su reloj digital, calculadora, TV, reproductor de DVD, y mucho más.
ELECTRÓNICA EMBARCADA – Todos los vehículos modernos cuentan con un microcontrolador que gestiona el funcionamiento de sus piezas, desde el motor hasta los sistemas de seguridad y navegación, incluyendo GPS y sistemas de entretenimiento.
ELECTRÓNICA MÉDICA – Una gran cantidad de equipos médicos utiliza los recursos digitales en su control, con un alto grado de sofisticación, por la capacidad de los circuitos empleados. Son equipos de rayos X, tomografía, etc.
loT – Internet de las cosas – circuitos digitales de Procesamiento, la interconexión y las comunicaciones de aparatos de todos los tipos conectados a Internet son digitales.

1.2 – Lógica digital
Todo el equipo que utiliza los circuitos digitales funciona obedeciendo un tipo de comportamiento basado en lo que se llama Lógica.
La diferencia de los circuitos de amplificador ordinarios que simplemente amplifican, atenúan o realizan algún tipo de procesamiento de señal simple, los circuitos digitales no procesan las señales basándose en un simple propósito que se determina cuando son fabricados.
Los circuitos digitales de todos los equipos que hacen uso de esta tecnología son capaces de combinar las señales, tomando decisiones de acuerdo a un comportamiento lógico.
Es evidente que si el lector realmente quiere entender las cosas que ocurren con los circuitos digitales, debe dejar exactamente el aprendizaje del comportamiento que queremos que tengan, es decir, un comportamiento lógico y esto implica saber qué tipo de comportamiento es este.
Podemos decir que a partir de la lógica podemos sacar conclusiones de hechos conocidos, o tomar decisiones de hechos conocidos.
Por ejemplo, la decisión de "encender una lámpara cuando está oscuro" es una decisión lógica, porque la proposición y la conclusión son hechos relacionados.
Por el contrario, la decisión de "encender una lámpara porque está lloviendo" no es una decisión lógica, porque los hechos involucrados no están relacionados.
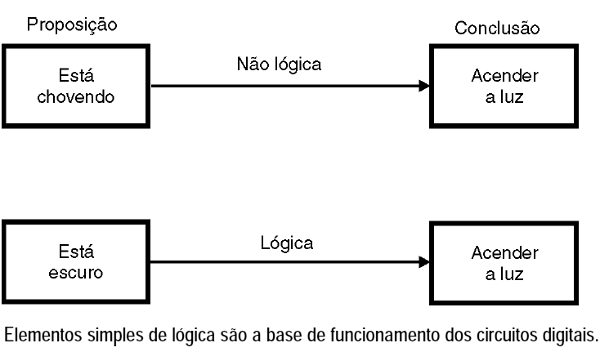
Otros ejemplos de lógica:
Accionar un relé cuando la temperatura alcanza un cierto valor
Sonar una campana cuando una pieza llega a cierta posición.
Abrir una puerta cuando se escribe la contraseña correcta en un teclado
Evidentemente, los hechos mencionados anteriormente son simples y sirven para ejemplificar cómo funcionan las cosas.
En la electrónica de los controles lógicos de la máquina, tales como microprocesadores, microcontroladores, DSPs y computadoras, lo que tenemos es la aplicación de la lógica digital, es decir, los circuitos que operan tomando decisiones de acuerdo a las cosas que suceden en su propio interior o en dispositivos que están conectados a ellos.
Los circuitos de lógica digital funcionan con señales eléctricas.
Así, los circuitos de lógica digital no hacen nada más que recibir señales con ciertas características y en su función toman decisiones que no son más que la producción de otra señal eléctrica.
Pero si las señales eléctricas son digitales, es que representan cantidades discretas, y si la lógica se basa en la toma de decisiones, el siguiente paso para entender la electrónica digital, con su lógica es precisamente ir a la forma en que las cantidades discretas son representado y entendido por los circuitos electrónicos.
1.3 – Sistemas de numeración
La forma en que contamos las cantidades proviene del hecho de que poseemos 10 dedos. Así, tomando los dedos de las manos, podemos contar objetos con facilidad hasta cierto punto.
El punto crítico se produce cuando tenemos cantidades mayores que 10. El hombre resolvió el problema indicando también la cantidad de manos, o veces cuando se usan los diez dedos.
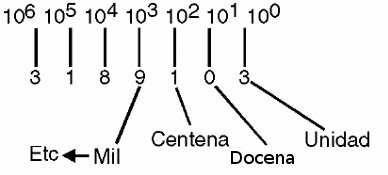
Así que cuando decimos que tenemos 27 objetos, el 2 indica que tenemos "dos veces las manos llenas" o dos decenas más 7 objetos. El 2 tiene un peso de 10.
Del mismo modo, cuando decimos que tenemos 237 objetos, el 2 ahora indica que tenemos "dos decenas de pares manos llenas "o 2 centenas mientras que el 3 indica que tenemos 3 pares más de manos llenas y finalmente el 7, más 7 objetos, como se muestra en la figura 3.
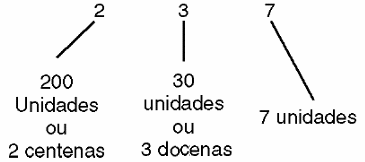
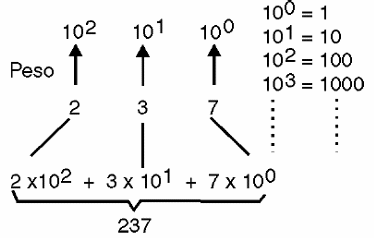
En otras palabras, la posición de los dígitos en la representación de los números tiene un peso y en nuestro sistema de numeración que es decimal este peso es 10, como se muestra en la figura 4.
¿Qué pasaría si tuviéramos un número diferente de dedos, por ejemplo, 2 en cada mano?
Esto significaría, en primer lugar, que en nuestro sistema base 4 (y no en la base 10) sólo habría 5 dígitos para representar los números: 0, 1, 2, 3 y 4, como se muestra en la figura 5.
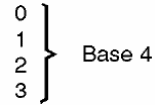
Para representar una cantidad mayor que 4, tendríamos que usar más de un dígito.
Por lo tanto, para indicar 7 objetos en la base 4, tendríamos "una mano completa con 4" y 3 más. Eso daría 13, como se muestra en la figura 6.
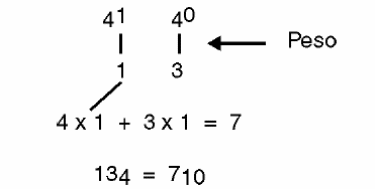
Vea entonces que en el "13" en la base 4, el 1 tiene el peso 4, mientras que el 3 tiene su valor normal.
Notación
Índice "4" en 134 Indica que el valor representado está en la base 4. Asimismo 710, el 10 indica que el valor representado está en la base 10.
De manera generalizada decimos que, dependiendo de la base del sistema, los dígitos tienen "pesos" que corresponden a su posición en el número, y que estos pesos son potencias de la base.
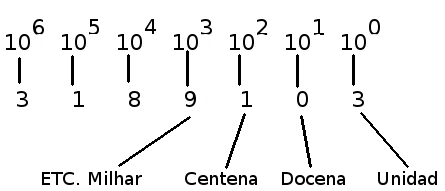
Por ejemplo, para la base 10, cada dígito de la derecha tiene un peso que es una potencia de 10 en orden ascendente, lo que nos lleva a la unidad (10 a la 1), a la diez (10 al exponente 1), a la centena (diez al cuadrado alto) , los mil (diez al cubo) y así sucesivamente, como se muestra en la figura 7.
En la electrónica digital, solemos decir que el dígito derecha, al representar la potencia más baja o tener menor peso, es el dígito (o bit *) menos significativo o LSB (Least Signficant Bit), mientras que aquel que está más a la izquierda es el más significativo o MSB (Most Significant Bit).
* El bit que es el dígito binario (en la base 2) se estudiará más tarde.
Para la base 4, los dígitos tienen potencias de 4 como se muestra en la figura 8.
De todas formas, permanece hasta hoy, como herencia de esos pueblos la división del año en 12 meses, del día a las 12 + 12 horas, las horas en 60 minutos y la misma docena
1.4 – Numeración Binaria
Los circuitos electrónicos no tienen dedos. También es evidente que no sería muy fácil proyectar circuitos que sean capaces de reconocer 10 niveles de una tensión, u otra magnitud eléctrica, sin el peligro de que cualquier pequeño problema haga que cause confusión.
Una pequeña variación de la tensión en estos circuitos puede cambiar de 3 a 4 o viceversa, afectando los cálculos que tiene que realizar.
Mucho más simple para los circuitos electrónicos es trabajar con un sistema de numeración que está más según su principio de funcionamiento y esto está hecho realmente.
Un circuito electrónico puede tener o no tener corriente, puede tener o no tener tensión, puede recibir o no un pulso eléctrico.
También es mucho más fácil diferenciar dos estados de elementos indicadores como una lámpara iluminada o apagada, un timbre silencioso o un timbre.
Sin embargo, los circuitos electrónicos son más apropiados para operar con señales que tienen dos condiciones posibles, es decir, que representan dos dígitos o números.
También podemos decir que las reglas que rigen el funcionamiento de los circuitos que operan con sólo dos condiciones posibles son mucho más sencillas.
Así, el sistema adoptado en los modernos circuitos electrónicos digitales es el sistema binario o base 2 donde sólo se utilizan dos dígitos, que corresponden a dos condiciones posibles de un circuito: 0 y 1.
Pero ¿cómo podemos representar cualquier cantidad utilizando sólo dos dígitos?
La idea básica es la misma utilizada en la representación de las cantidades en el sistema decimal: asignar pesos a los dígitos según su posición en el número.
Para entender mejor cómo funciona todo esto, vamos a tomar como ejemplo el valor 1101 que en binario representa el número 13 decimal (*) y ver cómo ocurre esto.
Así que cuando hablamos de 1101 en binario, simplemente escribimos 11012 y para representar 13 en decimal, escribimos 1310. Esta manera de indicar las bases de un número, será adoptada en nuestras lecciones de aquí en adelante.
El primer dígito de la derecha indica que tenemos una vez el peso de este dígito o 1. El cero del segundo dígito de derecha a izquierda indica que no tenemos nada con el peso 2. Ahora el tercer dígito de derecha a izquierda, y que tiene el peso 4, es un 1, lo que indica que tenemos "una vez cuatro". Finalmente el primer dígito de la izquierda que es un 1, y que está en la posición de peso 8, nos dice que tenemos "una vez ocho".
Sumando una vez ocho, con una vez cuatro y una vez uno, tenemos el total que es precisamente la cantidad que conocemos en decimal como trece.
Vea entonces que, como se muestra en la figura 9, en la numeración binaria, los dígitos tendrán pesos, de derecha a izquierda que son potenciales de 2, es, dos elevados al exponente cero que es uno, dos elevados al exponente 1 que es 2; Dos al cuadrado que es 4 y así sucesivamente.
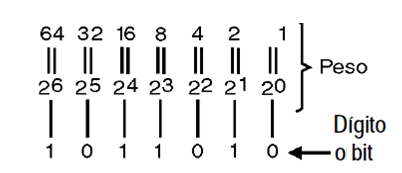
Para el lector, sólo recuerda que en cada dígito nos movemos a la izquierda, su peso se duplica, como se muestra en la figura 10.
Porque no hay límite a los valores de los pesos, esto significa que es posible representar cualquier cantidad en binario, no importa cuánto, simplemente usando la cantidad apropiada de dígitos.
Para 4 dígitos podemos representar números hasta 15; para 8 dígitos podemos subir a 255; para 16 dígitos podemos subir a 65 535 y así sucesivamente.
El lector debe recordar estos valores límites para 4, 8, 16 y 32 dígitos de un número binario, ya que tienen una gran importancia en las aplicaciones digitales modernas.
A continuación le damos la representación binaria de los números decimales hasta 17 para que el lector tenga una idea de cómo funciona todo:
decimal = binário
0= 0
1= 1
2= 10
3= 11
4= 100
5= 101
6= 110
7= 111
8= 1000
9= 1001
10= 1010
11= 1011
12= 1100
13= 1101
14= 1110
15= 1111
16= 10000
17= 100001 ... etc.
Para el lector que tiene la intención de entender la electrónica digital aplicada a las computadoras, equipos industriales, médicos y muchos diamantes hay momentos en que es necesario saber cómo convertir una indicación binaria al decimal correspondiente.
Podemos dar como ejemplo el caso de ciertas placas que se utilizan en el diagnóstico de ordenadores y máquinas industriales que tienen un conjunto de LEDs que se iluminan indicando un número correspondiente a un código de error.
Los LEDs borrados indican el dígito 0 y los LEDs iluminados indican el dígito 1, como se muestra en el ejemplo de la figura 11, donde tenemos una placa de display y un juego de 4 LEDs para indicación en binario.

Supongamos que en un diagnóstico la secuencia de disparo de luz de los LEDs es 1010. Desde el principio el lector necesita saber dónde empezar a leer, es decir, si el peso inferior es el derecho o el izquierdo.
En las indicaciones dadas por instrumentos o incluso en la representación de los valores binarios, por ejemplo, en la salida de un circuito es necesario saber cuál de los dígitos tiene mayor peso y que tienen menor peso.
Esto se hace con un acrónimo que se adopta normalmente y que se nombra al dígito, en el caso llamado bit.
Por lo tanto, para el dígito de menor peso significativo se adopta la sigla LSB (Least Significante Bit ) y para el más significativo se adopta MSB (Most Significant Bit ), como se muestra en la figura 12.

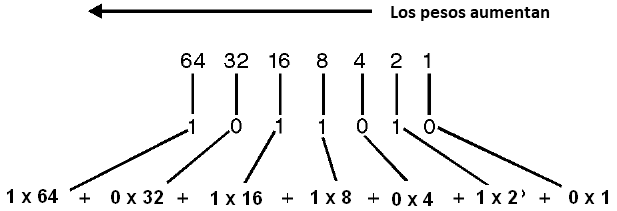
Lo que hacemos es sumar los valores dados por los dígitos multiplicados por el peso de su posición. En el caso del valor tomado como ejemplo, 1010110, tenemos:
Dígito x Peso = Valor
1 x 64 = 64
0 x 32 = 0
1 x 16 = 16
0 x 8 = 0
1 x 4 = 4
1 x 2 = 2
0 x 1 = 0
Sumando los valores tenemos:
64 + 16 + 4 + 2 = 86
El valor decimal de 1010110 es 86, o utilizando la notación más adecuada:
10101102 = 8610
Tenga en cuenta que para hacer una conversión, todo lo que el lector tiene que hacer es recordar que en cada dígito saltamos a la izquierda su peso se duplica en secuencia 1, 2, 4, 8, 16, 32, 64, 128, etc.
En la práctica, el problema inverso también puede ocurrir que es la transformación de un valor expresado en decimal (base 10) para la base 2 o binario.
Para esta transformación podemos hacer uso de un algoritmo muy simple que memorizado por el lector puede ser de gran utilidad, dada su practicidad.
Veamos entonces cómo usar el algoritmo para convertir un decimal a binario, como 116. Lo que hacemos es una serie de divisiones sucesivas, como se muestra en la figura 13.
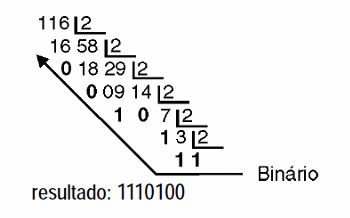
Vea entonces que dividimos los números por 2 hasta el punto en que alcanzamos un valor menor que 2 y que por lo tanto ya no se puede dividir.
El resultado de esta última división, es, su cociente es entonces el primer dígito binario del número convertido. Los dígitos restantes se obtienen leyendo los restos de derecha a izquierda de la serie de divisiones que realizamos. Todo muy simple y rápido.
1.4.1 - kilo, Mega y Giga
En electrónica digital, así como en la electrónica analógica tradicional, es común utilizar prefijos para representar cantidades muy grandes o muy pequeñas.
De esta manera, el kilo (K) prefijos para representar a miles, mega (M) para representar a millones y Giga (G) para representar billones también se utilizan en la electrónica digital.
Sin embargo, de manera diferente a lo que ocurre con la electrónica analógica, estos prefijos representan cantidades "levemente" diferentes.
Lo que ocurre es que cuando usamos kilo (k) para representar 1 000 (mil), en base 10, 1000 es un valor entero, el cual no ocurre con base 2.
Por lo tanto, el valor más cercano de la base 2 es 1024. Esto significa que, en la electrónica digital, el valor de kilo representa realmente 1024. Una memoria que tiene una capacidad de almacenamiento de 1 kilo bit o 1 kb en realidad almacena 1024 bits.
Del mismo modo, cuando decimos que un programa de computadora requiere un espacio de memoria de 1 megabytes, en realidad requiere un espacio de 1 048 576 bytes, ya que la potencia de 2 más cercana a 1 millón es 1 048 576.
En otras palabras, para informática y electrónica digital el kilo (k) vale 1024, el mega (M) vale 1 048 576 y el Giga vale 1 073 741 824.
1.5 – Binarios menos de 1
Para el lector, puede ser difícil entender cómo utilizar cantidades que sólo pueden ser completas, como lo indica la definición de digital al principio de esta lección, Es posible representar cantidades más pequeñas que una, es decir, "quebradas" o números fraccionarios.
Por supuesto esto es posible en la práctica, porque si no fuera por las computadoras, el control digital y el equipo de automatización y las calculadoras no podían realizar ninguna operación con estos números y sabemos que eso no es cierto.
Lo que se hace es utilizar un dispositivo que consiste en emplear potencias negativos de un entero, para representar cantidades que no son completas. De esta forma, se pueden utilizar dígitos binarios para representar cantidades fraccionarias sin problemas.
Vamos a dar un ejemplo tomando como ejemplo el número 0,01101 en binario.
La existencia misma de un "0", ya sugiere que es un número inferior a 1 y por lo tanto fraccional.
Lo que pasa es que los dígitos de este número tienen pesos que corresponden para las potencias de 2 negativas, y que no hay nada más que fracciones, de acuerdo con la siguiente secuencia:
Dígito x Peso = Valor
0, x 1 0
0 x 1/2 0,5
1 x 1/4 0,25
1 x 1/8 0,125
0 x 1/16 0,0625
1 x 1/32 0,03125
Sumamos los valores relativos que tenemos:
0,25 + 0,0625 + 0,03125 = 0,625
El número decimal representado es por lo tanto 0,625.
Vea que usando tantos dígitos como sea necesario podemos representar con cualquier precisión un número decimal menos de 1.
1.6 – Diferentes formas de usar el sistema binario
El uso de circuitos electrónicos con ciertas características, y la necesidad misma de adaptar el sistema binario a la representación de valores que se convierten rápidamente al decimal, e incluso a otros sistemas, llevó a la aparición de algunos Diferentes formas de usar los binarios llamados "puros".
Estas formas se encuentran en varios tipos de equipos digitales, incluidos los propios ordenadores.
1.6.1 - Sistema BCD (Decimal Codificado en Binario)
BCD es la abreviatura de Binary Coded Decimal y se adapta mejor a los circuitos digitales por las características que serán más claras a través de nuestro curso.
Lo que se hace es transformar cada dígito decimal de un número en un grupo binario de cuatro dígitos (bits), independientemente del valor total del número que se representará.
Así, partimos de la siguiente tabla:
Dígito decimal = BCD
0= 0000
1= 0001
2= 0010
3= 0011
4= 0100
5= 0101
6= 0110
7= 0111
8= 1000
9= 1001
Así, si queremos representar en BCD el número 23,25 no lo convertimos de la forma convencional por divisiones sucesivas Pero sí, tomamos cada dígito decimal y lo convertimos al BCD equivalente de la siguiente manera:
2 | 3 | 2 | 5
0010 | 0011 | 0010 | 0101
Vea entonces que para cada dígito decimal siempre tendremos cuatro dígitos binarios o bits y también que los valores 1010, 1011, 1100, 1101 y 1111 no existen en este código.
Esta representación fue muy interesante cuando las calculadoras se popularizaron, ya que podría ser utilizado para todas las operaciones con números comunes y los 5 códigos que no se utilizaron a partir de los valores que ¡no existían se adoptan para indicar las operaciones! (figura 14)
Usando representaciones de esta manera, ellos operaban los primeros ordenadores que eran muy apropiados llamados computadoras de "4 bits".
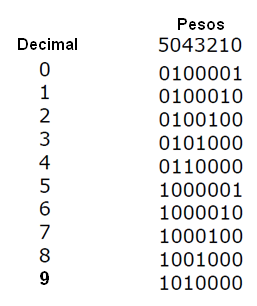
1.6.2 – Código Biquinário
Hay varios otros códigos utilizados en los equipos electrónicos digitales que merecen ser resaltados. Otro de ellos es el Código Biquinário
En este código tenemos 7 bits con diferentes pesos. Los primeros dos bits. o dígitos. Indique si el número está entre 0 y 5 o entre 5 y 9.
Por ejemplo, si el número es 7, tenemos en los dos primeros bits 1 y 0, porque el número es mayor que 5. Los otros bits indican, cuánto debe ser agregado a los 5 para conseguir el 7. Por lo tanto, usamos el bit de peso 2 para este propósito porque:
5 + 7 = 7
Entonces tenemos como representación del valor 7 en este código
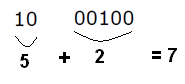
La tabla siguiente nos da las representaciones de los decimales de 0 a 9 en este código.
1.6.3 – Código Desbordamiento 3 (XS3)
Podemos decir que esta es una variación de BCD. En él, la diferencia es que con cada dígito representado, 3 se añade al valor correspondiente en BCD, como se muestra en la siguiente tabla.
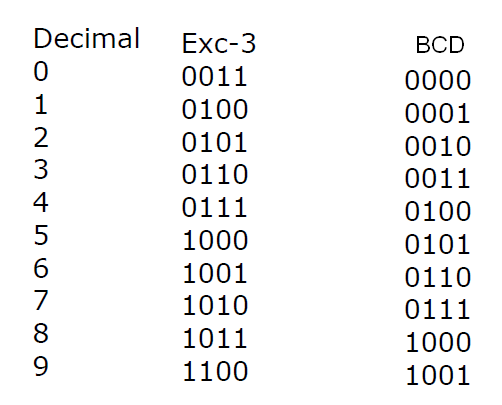
Vea entonces que, para representar el valor 5, sumamos 3, y con esto usamos BCD 8 (1000).
La ventaja de utilizar este código es la facilidad con la que se puede utilizar en operaciones matemáticas.
1.6.4 – Código Gray
El código Gray se caracteriza por el hecho de que el paso de cualquier número a lo siguiente se hace siempre con el cambio de un solo dígito.
Así, por ejemplo, cuando pasamos de 0111 (7 en decimal) a 1000 (8 en decimal) los cuatro dígitos cambian. En el código Gray el paso de 7 a 8 cambia sólo un dígito como el 7 ' 0100 y el 8 ' 1100.
La ventaja de cambiar un solo dígito, en el paso de un número al siguiente (o de vuelta a la anterior), es la posibilidad de tener mayor velocidad de circuitos y menor consumo. Como veremos en las próximas lecciones, el consumo de un circuito digital se produce principalmente, en el momento en que realiza una operación lógica, es decir, cambios de estado.
Una aplicación de este código se encuentra en los codificadores ópticos, que son dispositivos ópticos en los que tiene una codificación a través de zonas claras y oscuras que permiten medir su velocidad de rotación, o incluso determinar su posición, como se muestra en la figura 15.
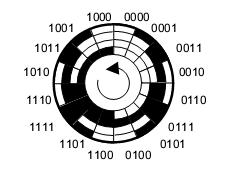
En la tabla siguiente tenemos algunos valores decimales, y los binarios correspondientes y el código Gray.
|
Decimal |
Binário |
Gray |
|
0 |
0000 |
0000 |
|
1 |
0001 |
0001 |
|
2 |
0010 |
0011 |
|
3 |
0011 |
0010 |
|
4 |
0100 |
0110 |
|
5 |
0101 |
0111 |
|
6 |
0110 |
0101 |
|
7 |
0111 |
0100 |
|
8 |
1000 |
1100 |
|
9 |
1001 |
1101 |
|
10 |
1010 |
1111 |
|
11 |
1011 |
1110 |
|
12 |
1100 |
1010 |
|
13 |
1101 |
1011 |
|
14 |
1110 |
1001 |
|
15 |
1111 |
1000 |
1.6.5 – Código 987654321
En el código 9876543210, tenemos una descodificación de "una salida de 10", o sea, un solo bit será 1 mientras que los otros serán 0, según el dígito que se representará, de acuerdo con la siguiente tabla:
|
Decimal |
9876543210 |
|
0 |
0000000001 |
|
1 |
0000000010 |
|
2 |
0000000100 |
|
3 |
0000001000 |
|
4 |
0000010000 |
|
5 |
0000100000 |
|
6 |
0001000000 |
|
7 |
0010000000 |
|
8 |
0100000000 |
|
9 |
1000000000 |
La desventaja de este código es que necesitamos 8 bits para representar los dígitos 0 a 9.
1.6.7 - Códigos de error
En la transmisión de datos en forma digital, es extremadamente importante asegurar la integridad de la información. Para este propósito hay recursos que le permiten saber si un número en el formulario binario se transmitió correctamente o no. Para ello, se agregan códigos especiales, llamados códigos de error.
1.6.8 – Binario con Paridad
Una forma sencilla de detectar la integridad de un valor binario pasado en BCD es añadir un bit que indique la paridad. Así que este bit será 1, si la suma de los bits de los cuatro bits pasados es impar y será 0, si la suma es uniforme. Como ejemplo, damos dos casos posibles, donde p es el bit de paridad.

1.6.9 - Código 2 de 5
En este código siempre hay dos dígitos 1, como se muestra en la siguiente tabla:

De esta manera, si una transmisión de datos aparece un bloque de 5 bits con un número distinto de 2 bits 1, entonces usted puede saber que los datos han llegado incorrectamente.
1.7 - SISTEMA HEXADECIMAL
Los bits de los circuitos digitales se agrupan en conjuntos de 4, así (nibble), de esta manera tenemos los microprocesadores y ordenadores de 4, 8, 16 y 32 bits, etc.
También observamos que con 4 bits podemos obtener representaciones binarias de 16 números, no sólo 10. Vimos que el excedente 5 podía ser utilizado para representar operaciones en las calculadoras.
Esto significa que, mucho más compatible con la numeración binaria o la operación binaria de los circuitos digitales, como los ordenadores, es la representación de valores en el sistema hexadecimal o base 16.
Y, de hecho, esto se hace: abriendo muchos programas desde un ordenador vemos que sus características como las posiciones de memoria o la cantidad de memoria se hacen en este sistema.
Esto significa que todo aquel que trabaje con la electrónica digital necesita conocer este sistema y, más que eso, saber hacer conversiones desde ella hasta el decimal y viceversa además de conversiones al sistema binario.
En la tabla siguiente damos las representaciones de los dígitos de este sistema con equivalentes decimal y binario:
| Decimal | Binário | Hexadecimal |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
En la figura 16 tenemos la presentación de valores de 0 a 15 en pantallas de 7 segmentos, utilizando codificación hexadecimal.

Tenga en cuenta que, dado que no hay símbolos para los dígitos de 10, 11, 12, 13, 14 y 15, se han utilizado las letras A, B, C, D, E y F.
Cómo hacer conversiones: los mismos procedimientos que hemos visto en el caso de las conversiones de decimal a binario y viceversa son válidos para el caso del hexadecimal cambiando sólo la base.
Vamos a dar ejemplos:
Cómo convertir 4D5 a decimal:
Los pesos en el caso son: 256, 16 y 1. (en cada dígito a la izquierda multiplicamos el peso de la primera por 16 para obtener un nuevo peso).
Tenemos entonces:
4D5 = (4 x 256) + (13 x 16) + (1 x 5) = 1237
Tenga en cuenta que la "D" corresponde a 13. El número decimal equivalente a la 4D5 hexadecimal o "hex" como se representa a menudo, es 1237.
4D5 (hex) = 1237 (dec)
La conversión inversa, esto es, de decimal a hexadecimal se hace por divisiones sucesivas. Tome el caso de 1256, que se muestra en la figura 17.
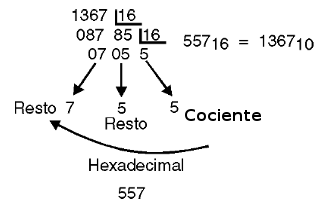
Vea entonces que usted acaba de leer el cociente final y luego los remanentes de las divisiones sucesivas, siempre recordando que aquellos que superan los 10, deben ser "intercambiados" por las letras equivalentes.
1.8 – Aritmética Binaria
De la misma manera que podemos realizar operaciones con decimales, también podemos sumar, sustraer, multiplicar o dividir números binarios.
Para trabajar con números binarios los procedimientos (algoritmos) son bastante similares a los utilizados con los números decimales y, por supuesto, podemos aplicar estos procedimientos a los números en cualquier base.
Para realizar operaciones aritméticas con números binarios sólo hay que recordar algunas reglas básicas que se dan a continuación:
Las operaciones con números binarios siguen ciertas reglas que se indican a continuación:
a) Sume:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (va uno)
b) sustracción:
0-0 = 0
0-1 = 1 (preste 1)
1-0 = 1
1-1 = 0
c) Multiplicación:
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
d) División:
0:0 = 0
0:1 = 0
1:0 = no permitido
1:1 = 1
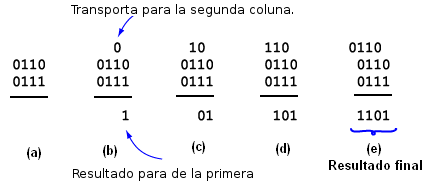
Vamos a tomar la suma binaria de 6 (0110) con 7 (1110) como ejemplo. Colocando un número en el otro, como en la figura 18 (a).
Sumando la última columna de la derecha, siguiendo las reglas dadas anteriormente, tenemos que 0 + 1 = 1 y "va 0" para ser transportados a la segunda columna, como se muestra en la figura 18 (b)
A continuación se suman los tres dígitos de la segunda columna: 0 + 1 + 1 = 1 y "va 1", que se transporta a la tercera columna, como vemos en la figura 18 (c).
Ahora sumamos los tres dígitos de la tercera columna 1 + 1 + 1 = 1 y "va 1", que se transporta a la cuarta columna, como se muestra en la figura 18 (d).
Finalmente sumamos los dígitos de la cuarta columna: 1 + 0 + 0 = 1 y "va 0". Con esto conseguimos resultado final en la figura 18 (e)
Es fácil entonces convertir 1101, que es el resultado final, en decimal, alcanzando el resultado esperado: 13.
A continuación se muestra un ejemplo de sustracción binaria. Note que en la primera columna, como no podemos tomar 1 de 0, "prestamos 1" de la segunda columna (de derecha a izquierda), exactamente como lo hacemos con los números decimales. En la figura 19 tenemos un ejemplo de sustracción binaria.
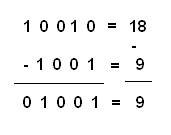
Para la multiplicación, podemos dar el siguiente ejemplo, observando, que de la misma manera que en la multiplicación decimal, multiplicamos los números de la primera fila por cada una de la segunda fila, como se muestra en la figura 20.
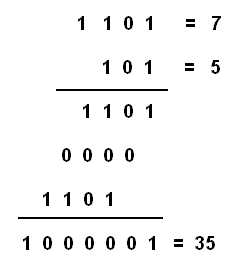
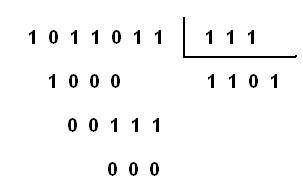
Finalmente podemos dar un ejemplo de división binaria en la figura 21:
Hay procesos de cálculos sencillos que se realizan con los complementos. Los complementos de un número son la diferencia entre la base y el número. Por ejemplo:
El complemento de 3 en base 10 es 7
El complemento de 1 en base 2 es 1
El complemento de 2 en base 2 es 0
En la siguiente lección veremos cómo estas operaciones se pueden utilizar más eficazmente a través de lo que llamamos Álgebra Booleana.
Sumário
Curso de Electrónica - Electrónica Digital (CUR5000)
Curso de Electrónica - Electrónica Digital – Parte 1 (CUR5001S)
Curso de Electrónica Digital – Parte 2 - El Álgebra de Boole (CUR5002S)
Curso de Electrónica - Electrónica Digital - Parte 6 - Los Elementos Biestables (CUR5006S)
Curso de Electrónica - Electrónica Digital - Parte 9 - Contadores Digitales (CUR6002S)
Curso de Electrónica - Electrónica Digital - Parte 13 - Memorias, ADCs y DACs (CUR6006S)



