Electrónica de potencia
Cuando hablamos de electrónica de potencia nos referimos a circuitos y dispositivos que operan con intensas corrientes y eventualmente altas tensiones, dando como resultado el manejo de potencias elevadas.
Como estos circuitos y dispositivos se encuentran generalmente en las industrias, en el control de la maquinaria pesada y del otro automatismo, es común que esta rama de la electrónica también se trata como electrónica industrial, automatización industrial, o incluso mecatrónica.
El término Mecatrónica se debe al hecho de que en la mayoría de los casos los dispositivos y circuitos de potencia se utilizan para controlar equipos mecánicos como maquinaria industrial, automatismo, vehículos, brazos robóticos, robots autónomos, etc.
Así, en este curso tratamos inicialmente con dispositivos electrónicos y componentes que operan con corrientes intensas y eventualmente altas tensiones, manejando potencias elevadas.
También observamos que muchos de los dispositivos que abordaremos no manejan potencias elevadas, sino que se utilizan en el control de dispositivos de alta potencia, por lo que es importante incluirlas en nuestros estudios.
En este grupo, se enmarcan pequeños dispositivos como Diacs, SIDACs, Sus, SBS, etc.
Finalmente recordamos que los conceptos básicos utilizados en este libro fueron estudiados en los volúmenes anteriores de esta serie, en particular el Curso de Electrónica - Electrónica Básica - Vol. 1, y Curso de Electrónica – Electrónica Analógica – Vol. 2 – del mismo autor.
Unidades Eléctricas
En este punto realizaremos una pequeña revisión de las principales unidades eléctricas, con énfasis en la corriente, tensión y potencia, cuyo conocimiento debe estar muy bien definido, de manera que no tenga dudas en la comprensión del principio de funcionamiento de los componentes y circuitos de energía.
Principio de Conservación de Energía
Un principio muy importante que a menudo se recordará cuando se estudian los fenómenos eléctricos es la conservación de la energía. Este principio afirma que la energía no puede ser creada o destruida, siempre conserva.
Así que cuando una batería alimenta una lámpara, la luz producida tiene la misma cantidad de energía que la batería gasta para ello. De manera similar, si usted tiene un amplificador, la cantidad de sonido obtenida (energía) es la misma que la cantidad de energía eléctrica que consume cuando está enchufada en el tomacorriente.
En otras palabras, en los procesos que estudiamos que involucran la electricidad, la cantidad de energía presente siempre será la misma. Va a ir de un tipo a otro, lo que significa que va a girar.
Vea en la figura 1 un ejemplo, en el que la energía química liberada dentro de la pila se convierte en energía eléctrica que luego alimenta una lámpara convirtiéndose en energía luminosa (luz) y calor (la lámpara se calienta). Si medimos la cantidad de luz y calor producida por la lámpara, veremos qué es exactamente igual a la cantidad de energía liberada en el proceso químico dentro de la batería.
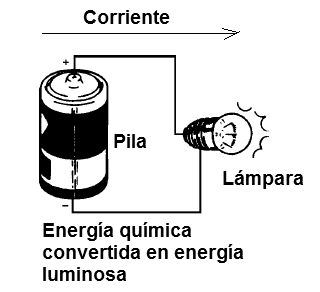
Comprensión de las unidades - Corriente, Voltaje y Energía
Es un hecho inaceptable que muchos profesionales de la electrónica pueden confundir magnitudes eléctricas, tales como corriente, tensión y potencia. Usando estas magnitudes de la manera incorrecta se puede causar serios problemas de funcionamiento de un equipo o incluso comprometer la seguridad y lo que puede ser mucho más grave: descréditos de la competencia de los profesionales o cualquier profesional de la electrónica.
Es común ver a profesionales usando forma totalmente incorrecta las magnitudes eléctricas, tensión confusa, corriente y energía.
¿Quién no ha oído a un profesional "competente" decir que cual dispositivo funciona con una "corriente" de 110 V o algo así?
¡Para un estudiante de electrónica que hace tal declaración lo menos que se recomienda es un cero o un buen castigo!
Incluso algunos que ya no hacen este tipo de cita a veces pueden tener dudas que muestran que la confusión sobre la corriente, tensión y también la potencia persiste en muchos casos.
Es el caso de algunos lectores que se preguntan cómo una fuente que proporciona una tensión de salida de 12 V bajo corriente de 2 Ampere máximo tiene su entrada protegida por un fusible de sólo 500 mA, colocado en la línea de 110 V.
Tratando de eliminar definitivamente las dudas de los lectores y evitar alguna confusión que tenemos este Artículo Que ciertamente no es bueno para los ingenieros y técnicos de alto nivel que son atentos y actualizado, aparte de los que andan un poco olvidados o quieren reciclar el conocimiento (que siempre es bueno), lo que ayudaría mucho a entender mejor los diferentes capítulos de este libro.
CORRIENTE Y TENSIÓN (*)
Una corriente es un flujo de cargas eléctricas.
Electrones libres que se mueven en un alambre de cobre forman una corriente eléctrica.
La medida de esta corriente se hace de acuerdo con la cantidad de electrones o cargas que pasan a través de un punto de ese alambre en cada instante, como se muestra en la figura 2.
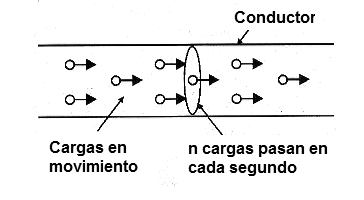
Cuantas más cargas pasan a través de este punto, mayor es la intensidad de la corriente.
Decimos cargas y no simplemente electrones, porque como sabemos, la corriente puede ser obtenida cuando los electrones libres se mueven en un sentido, caso de un metal, como huecos o lacunas en la dirección opuesta como, Por ejemplo, en un semiconductor de tipo P.
Para medir esta corriente, la unidad utilizada es el ampère (A).
Un ampère (1 A) corresponde a una cantidad de cargas equivalentes a 1 Coulomb (1 C) pasando por un punto de un conductor en cada segundo.
Llevando en cuenta que cada electrón (o hueco) tiene una carga de 1.6 x10-19 Coulomb, podemos tener una idea de cuántos electrones se están moviendo en un alambre y pasar por cierto tramo de esta cuando una corriente de 1 A se está llevando a cabo.
Si los lectores piensan que la velocidad de estos electrones es demasiado grande, se equivocan.
Aquí es donde entra en el concepto de tensión.
Como una corriente de agua en una tubería, la electricidad necesita ser "empujada" por una fuerza externa.
La acción externa responsable de esto es precisamente la tensión.
Así que tenemos varias formas de expresar esta fuerza externa:
Una es tomar como referencia la diferencia de presión que existe entre los extremos de un alambre, donde se establece la corriente, como se muestra en la figura 3.
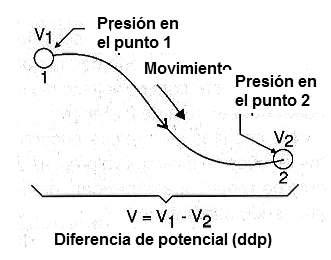
Es como si tuviéramos un reservorio de agua de 10 metros de altura y establecemos un flujo de agua a través de una tubería con la salida a 5 metros de altura.
La diferencia entre los niveles de agua o presiones es de 5 metros, como se muestra en la figura 4.
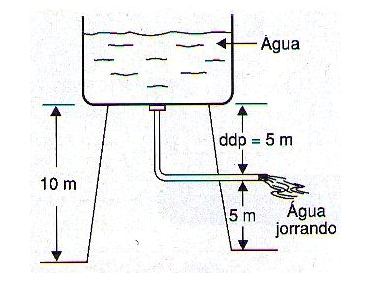
Para la electricidad podemos tener la caja de agua en un potencial de 10 volts y el extremo del alambre en un potencial de 5 volts de modo que la diferencia potencial o d.d.p. Será de 5 volts.
En otras palabras, podemos indicar como causa para la circulación de una corriente la diferencia de potencial entre los extremos de un alambre o circuito.
Otra manera es siempre expresar la presión que podemos tener en una tubería de agua tomando como referencia, por ejemplo, el nivel del mar, como se muestra en la figura 5.
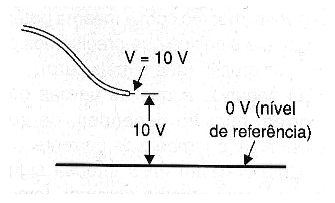
Al hacerlo, no vamos a necesitar saber cuál es el potencial en el que cada extremo del cable.
Podemos simplemente decir que el potencial o la tensión en el alambre es de tantos volts, refiriéndose a la fuerza disponible para empujar la corriente y teniendo en cuenta que el otro extremo está en el nivel de referencia o cero, como se muestra en la figura 6.
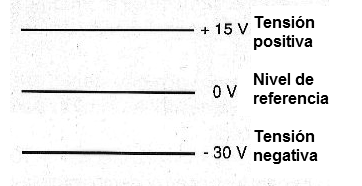
Sin tensión no hay circulación de corriente, pero hay una tensión que se puede manifestar sin corriente.
Entre los polos partir de una batería, por ejemplo, se manifiesta una diferencia de potencial, o sea, existe la posibilidad de que la batería aplique una tensión en un circuito.
Sin embargo, sólo habrá corriente en el momento en que se conecta a los polos de la pila un medio o un circuito donde la corriente puede fluir.
En una toma de corriente hay una "tensión" de 110 V, pero la corriente sólo existirá en el momento en que algún dispositivo esté conectado a esta toma de corriente.
CORRIENTE X TENSIÓN = ENERGÍA
La energía suministrada a un circuito eléctrico depende tanto de la tensión como de la corriente.
Es la "fuerza" con la cual las cargas eléctricas se empujan sobre un alambre y su cantidad que depende de la cantidad de energía que un circuito puede recibir en cada instante, es decir su potencia
Así, la energía eléctrica de un circuito, como se muestra en la figura 7, es dado por el producto de la tensión por la corriente.
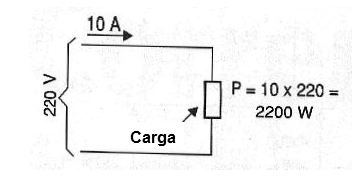
La potencia, que se mide en watts (W), es una característica de un circuito y por lo general no puede ser alterada.
Sin embargo, se puede modificar la forma en que se puede suministrar esta potencia al circuito.
Así, si un circuito necesita 100 watts para trabajar, podemos diseñarlo de tal manera que sea alimentado por 20 volts, en cuyo caso la corriente que circulará en funcionamiento normal (despreciando las pérdidas) será de 5 Ampere, ya que podemos diseñarlo para opere con 50 volts, en cuyo caso la corriente será de 2 ampères.
Y en la alimentación externa de los circuitos también tenemos varias posibilidades.
Si tenemos una ducha que debe funcionar con una potencia de 2 200 watts , que se considera razonable para dar una buena calefacción a un flujo normal de agua tenemos dos posibilidades de alimentarlo:
Si conectamos esta ducha a la red de 110 V, para obtener los 2 200 watts, la corriente que circulará será de 20 Amperes.
Si enchufamos la misma ducha en la red de 220 V, la corriente será de sólo 10 Amperes.
¡Usted ve que no estamos ahorrando energía en el segundo caso!
Pagamos por los watts multiplicados por el momento en que la ducha está encendida, y en ambos casos la potencia es de 2 200 watts.
Entonces, ¿cuál es la ventaja?
Los cables que llevan la energía eléctrica tienen una cierta resistencia que depende de su grueso y de su longitud.
Del mismo modo, dependiendo del espesor, los cables presentan una cierta limitación a la intensidad de la corriente que puede conducir.
Así que si usamos la red de 110 volts para transferir energía a una ducha y su instalación usando cables largos tenemos dos problemas a considerar.
La primera ' que la corriente debe ser el doble de grande que, si usamos 220 volts, incluso con la misma potencia, lo que significa que necesitamos un cable más grueso (que es más caro).
La segunda es que, las pérdidas que ocurren en un cable dependen de su resistencia y también de la corriente.
Una corriente más intensa significa que en la misma ruta tenemos mayores pérdidas de energía.
Vamos a dar un ejemplo numérico:
Digamos que para la ducha que a 110 volts requiere una corriente de 20 Ampere, tenemos que usar un cable que tiene una resistencia de 1 Ohm, como se muestra en la figura 8.
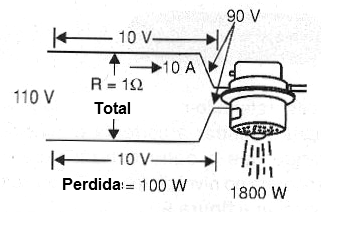
La caída de tensión ser dado para:
V = R x I
Donde:
V es la caída de tensión en el cable, es decir, la "disminución" de la tensión en el circuito en volts.
R es la resistencia del alambre en ohm
I es la intensidad de la corriente en Ampere
V = 1 x 20
V = 20 volts
Vea entonces que en la ducha sólo tendremos 90 volts en lugar de la 110 aplicada, porque 20 volts "se pierden" en los cables.
El poder que estos 20 Volts Representar también es preocupante:
P = V x I
Donde:
P es la energía disipada en el alambre en watts
V es la caída de tensión en el cable en volts
I es la intensidad actual en Ampere
P = 20 x 20
P = 400 watts
Ahora, esos 400 watts perdidos en la instalación se convertirán en calor, calentando los cables, ¡lo cual es realmente preocupante!
Si usamos 220 V en la misma ducha, incluso con una instalación que tiene 1 Ohm, las cosas cambian:
Recuerde que, en este caso, para obtener el 2 200 Watts la corriente será de 10 Amperes.
La caída de tensión sólo será de 10 volts, lo que significa que, en lugar de 220 V en la ducha, tendremos 210 volts.
La energía perdida en el alambre y disipada en forma de calor será:
Las pérdidas son mucho más pequeñas en este caso, es consecuentemente el calentamiento de la instalación.
Esta es la razón por la que damos preferencia a las tensiones más altas cuando debemos alimentar circuitos de alta potencia o transmitir energía eléctrica a través de cables largos.
Potencia continua y alterna
Una corriente que fluye siempre en la misma dirección y con la misma intensidad, como ocurre cuando conectamos una lámpara a una batería, se llama "corriente continua". Podemos abreviar esta designación por CC o incluso, utilizando el término americano " direct current“ por DC. En la figura 9 tenemos el gráfico que indica la intensidad de una corriente continua con el tiempo.
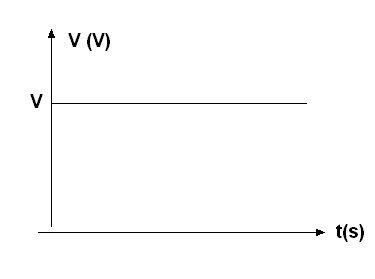
Nótese que para provocar una corriente continua necesitamos establecer en su circuito una tensión constante, esto es, una tensión que también es continua.
Sin embargo, en aplicaciones de energía que hacen uso de la energía de la red de distribución, el tipo de corriente encontrada es otro.
Esta corriente es generada por alternadores cuyo principio de funcionamiento ha sido analizado en nuestro curso de electrónica analógica (Vol. 2). El lector podrá revisar su principio de funcionamiento en esa edición del mismo autor.
A medida que estudiamos, en la salida de un alternador tenemos una corriente que varía entre máximo y mínimo regularmente, es decir, invierte constantemente la dirección de circulación, que corresponde a una corriente alterna.
Vemos entonces que, si conectamos un receptor a un generador de este tipo, la mitad del tiempo de un ciclo, la corriente circula en una dirección, y en la otra mitad circula en la dirección opuesta. La energía de la red pública y utilizada en las industrias y otras aplicaciones es de este tipo.
Como estudiamos anteriormente, podemos representar la corriente generada por este tipo de generador por una curva llamada sinusoidal, como se muestra en la figura 10.
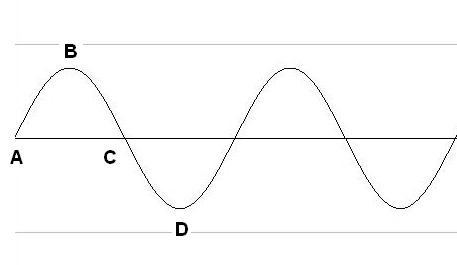
El generador que produce la energía que consumimos da 60 vueltas por segundo, Lo que significa que cada segundo la corriente circula 60 veces en una dirección y 60 veces en la dirección opuesta. Decimos que la corriente de la red pública que alimenta residencias, instalaciones comerciales e industriales y otras se alterna con una frecuencia de 60 Hertz (Hz).
Hay países, como Argentina, España, Chile, Paraguay, Uruguay y Bolivia donde la corriente generada tiene una frecuencia diferente, como 50 Hz. lo interesante es que los efectos obtenidos en la transmisión de energía utilizando corriente alterna son los mismos que se obtendrían con la corriente continua, con ventajas que estarán claros durante el curso. Vamos a tomar el siguiente ejemplo:
Pasando a través del filamento de una lámpara o elemento calefactor, los efectos finales son siempre los mismos: cuando se empuja, las cargas transfieren energía en forma de calor y cuando se tiran también, lo que significa que las lámparas se iluminan de la misma manera y los calentadores calientes de la misma manera.
Formas de Onda, Frecuencia, Fase y Valores
La representación gráfica de una corriente alterna tiene una forma muy especial: decimos que se trata de una forma de onda “sinusoidal” o “senoidal” , ya que estudiamos en el curso de la electrónica analógica.
Esto nos lleva a decir que la corriente alterna que se distribuye a las casas, el comercio y la industria se alterna con la forma de onda sinusoidal y la frecuencia de 60 Hz. analizando esta onda hay varios valores importantes que el profesional de la electricidad y La electrónica de potencia debe saberlo.
La primera, de la que ya hemos hablado, es la frecuencia que es el número de veces en cada segundo que se completa un ciclo de la generación de esa energía. La frecuencia se mide en Hertz (Hz). La duración de un ciclo completo nos da el período de corriente alterna.
Para una corriente alterna de 60 Hz, por ejemplo, el período o el tiempo de un ciclo completo es de 1/60 s, como se muestra en la figura 11.
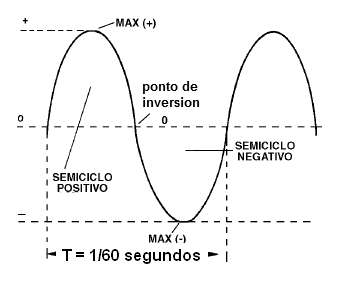
La amplitud de una tensión alterna se expresa de varias maneras, como podemos ver en la figura 12.
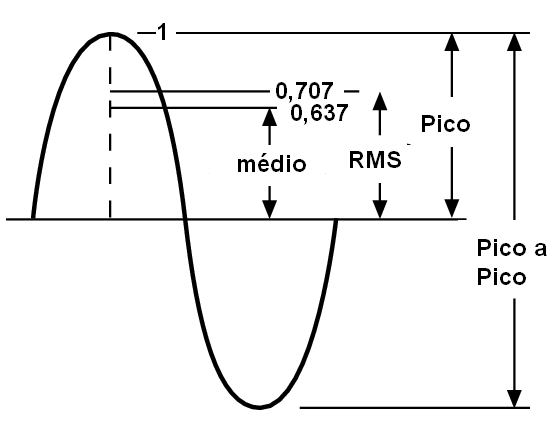
El valor máximo que alcanza una tensión alterna es el valor máximo. Indicamos este valor por Vp. La mitad del valor máximo nos da el valor medio o Vm.
Sin embargo, un valor muy importante es el "valor medio cuadrático" o " root mean square “del inglés, que nos lleva a la abreviatura Vrms. Este valor corresponde a la raíz cuadrada de 2 dividido por 2 veces el valor máximo, o como se muestra en la fórmula:
Vrms = 0707 x VP (f 7.2)
Donde:
Vrms es la tensión media cuadrática (en volts)
VP es la tensión máxima
0,707 es la raíz cuadrada de 2 (1,41) dividido por 2
Teniendo en cuenta que la raíz cuadrada de 2 es aproximadamente 1,41, dividiendo ese valor por 2, obtenemos 0,707. Eso significa que conseguimos la tensión RMS Multiplicando el pico de tensión por 0,707. De la misma manera, conociendo la tensión RMS obtenemos el valor máximo al multiplicarlo por 1,41.
La tensión de "110 V" que encontramos en la red eléctrica tiene este valor RMS. Así, el momento en que está en su máximo, el pico va a:
Rd = 1,41 x 110 = 155,1
Lo mismo ocurre con las intensidades de corriente: podemos hablar de la corriente máxima (IP), corriente media (Im) y la corriente RMS (IRMS) en un circuito.
Otro valor importante que debemos observar en la representación de una tensión o corriente sinusoidal es su fase. Cada momento, dentro de un ciclo, la tensión alterna tiene un cierto valor. Este valor cambia constantemente, dependiendo de la frecuencia de la tensión alterna.
En ciertas aplicaciones es importante conocer el valor que la tensión o corriente en un circuito de corriente alterna asume en un momento determinado dentro del ciclo.
Para ello, lo que se hace es dividir el ciclo a 360 grados (como en una circunferencia) e indicar el instante por un ángulo entre 0 y 360, como puede ver el lector en la figura 13.
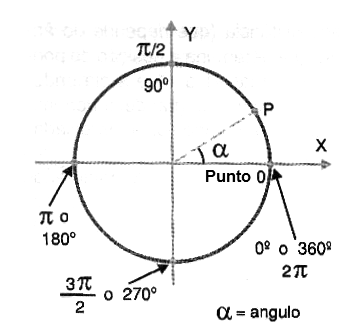
Los 360 grados se adoptan recordando que un ciclo de una corriente alterna se genera en un giro completo del alternador. De esta manera se puede indicar el momento deseado en un ciclo por un ángulo de fase, dado en grados.
También podemos utilizar el mismo concepto para comparar dos corrientes alternas o tensiones que no están perfectamente sincronizadas, es, que no alcanzan los puntos máximo y mínimo en el mismo instante.
Decimos que estas corrientes están "desfasadas" y podemos indicar la diferencia de fase entre ellos por un ángulo, como se puede observar en la figura 14.
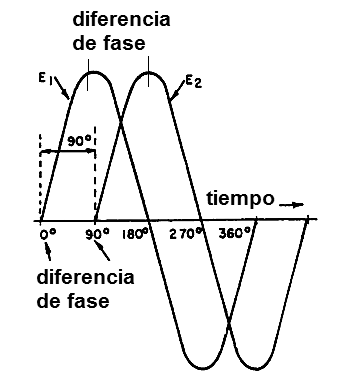
Alternadores
Los alternadores son generadores que convierten la energía mecánica en energía eléctrica. En el caso específico de estos generadores, la energía se pone disponible en forma de corrientes alternas. Encontramos los alternadores en diversas aplicaciones, tales como centrales hidroeléctricas y automóviles.
Tanto en las plantas como en los alternadores de coches básicamente tenemos dos sets de carretes. Un conjunto de rotor que gira para cortar las líneas de fuerza del campo magnético y un conjunto estacionario que crea el campo magnético, pero no se mueve.
Energía bifásica y trifásica
La energía que recibimos en nuestra casa viene en forma de una tensión alterna que depende de la configuración de la red.
En un primer caso tenemos la configuración de 220 V triángulo en la que entre cada fase la tensión es de 220 V y entre el neutro y la fase la tensión es 110 V con una configuración de estrella. La figura 15 muestra lo que sucede.
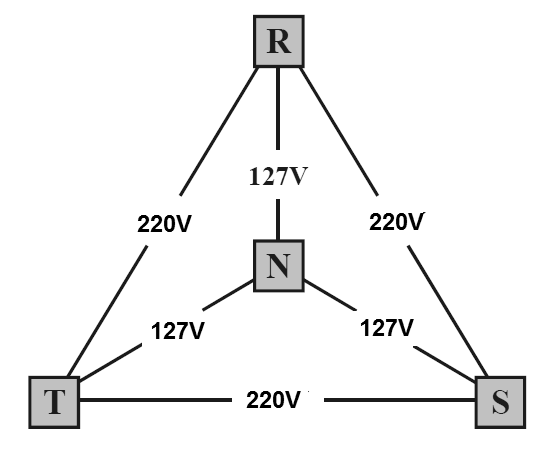
En un segundo caso tenemos la red a 380 V, donde la tensión entre fases es de 380 V, con la configuración triángulo, y entre cada fase y el neutro tenemos 220 V, en la configuración de estrella, que se muestra en la figura 16.
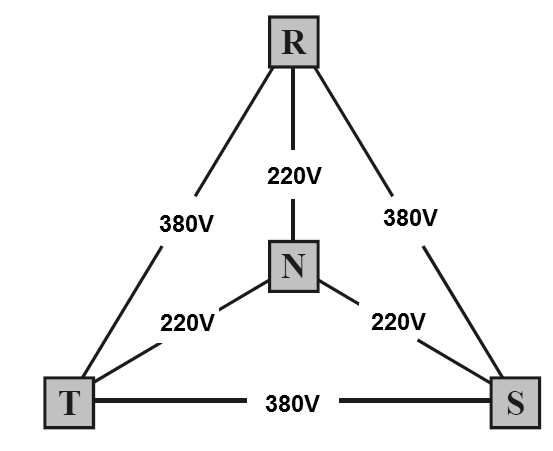
En los usos industriales y de energía la energía se hace disponible en forma trifásica. Esta forma de generar y distribuir energía en sistemas de corriente alterna se emplea principalmente en la industria, por diversas razones como, por ejemplo, la mayor conveniencia en la alimentación de motores eléctricos de alta potencia. Vea la figura 17.
En este sistema Se generan tres voltajes con diferencias de fase de 120 grados, como se muestra en la figura 17.
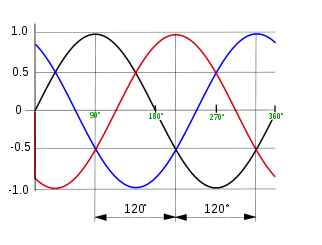
Lo que usted hace para esto es utilizar un sistema de generador donde usted tiene tres tensiones alternas disponibles en diferentes carretes, como se muestra en la figura 18.
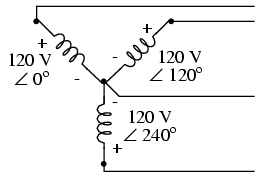
Cada una de las bobinas, que tiene un extremo conectado a un polo neutro común, ofrece una tensión sinusoidal ligeramente desfasada en relación con la otra.
Energía Activa y Energía reactiva
La potencia activa es la que efectivamente realiza un trabajo siendo completamente convertida en luz, calor, movimiento, etc. Esta potencia se mide en W (Watt) y sus múltiplos (kW o MW).
Un ejemplo de una carga que consume completamente la energía suministrada es una lámpara incandescente. Representa una carga de resistencia pura (óhmica), como se muestra en la figura 19, pues en ella la corriente y la tensión están en fase.
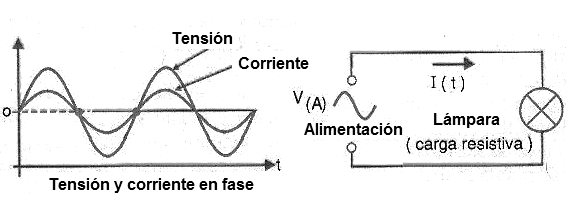
Sin embargo, en muchas aplicaciones encontramos cargas que no son resistivas puras, sino reactivas (capacitores e inductores) como es el caso de los motores.
En una carga de este tipo, la potencia es reactiva y se mide en VAR (Volt - ampere reactivo) o sus múltiplos (kvar y Mvar), como se muestra en la figura 20.
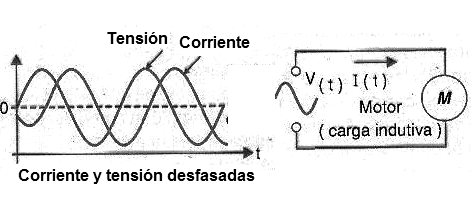
Lo que pasa es que, en los inductores, la potencia reactiva no se utiliza en la producción de trabajo, ya que sólo tiene la función de establecer los campos magnéticos.
Esa potencia, sin explotar, podría ser usado para propósitos mejores en una instalación industrial. La suma vectorial de la potencia activa con la potencia reactiva nos da la potencia real, como se muestra en la figura 21.
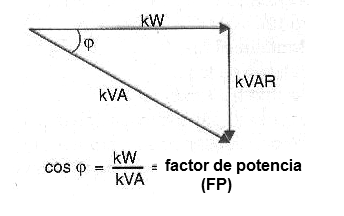
Vea que, si la potencia reactiva es pequeña, el ángulo entre la potencia real y la potencia activa disminuye, lo que indica un uso más eficiente de la energía.
Así, en lugar de especificar la potencia activa o potencia reactiva, es común indicar la eficiencia en el suministro y uso de energía por el coseno del ángulo mostrado en la figura 21. Este ángulo, llamado φ (Phi), una letra griega que se pronuncia "Fi", ha Su coseno se acerca a 1 cuando tiende a cero y establece el factor de potencia.
Por aquí, teniendo en cuenta que, en la figura, este ángulo puede tomar valores entre 0 y 90 grados, su coseno varía entre 0 y 1, como se muestra en la figura 22.
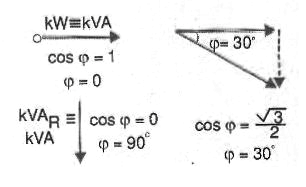
Podemos entonces decir que el coseno de φ puede variar entre 0 y 1. Mucho mejor será el uso de energía cuanto más cerca esté el factor de potencia (FP) está cerca de 1, que es el valor ideal.
También es posible medir el factor de potencia como la relación entre la potencia activa y la reactiva.
Así, en las facturas de energía tenemos la especificación de KVA, sino más bien la Kvarh (kilowatts - reactivo x hora) y kWh (kilowatts x hora).
Es importante tener en cuenta que todo esto es válido cuando la energía está dentro de los estándares de calidad que estas aplicaciones requieren.
Impedancia
Cuando tratamos con circuitos que sólo usan resistencias puras, es, componentes que se comportan como resistencias, podemos aplicar la ley de Ohm, sin problema, para calcular su comportamiento eléctrico.
Sin embargo, si tenemos un circuito de corriente alterna y en vez de apenas resistores justas también encontramos inductores y capacitores, la ley de Ohm, como la conocemos, ya no vale.
Si sólo tenemos capacitores o sólo inductores, podemos utilizar las fórmulas de reactancia capacitiva e inductiva, a medida que estudiamos, pero todo esto cambia cuando combinamos estos componentes, obteniendo así circuitos RLC.
Si, por un lado, los capacitores tienen la corriente por adelantado en relación con la tensión y los inductores retrasan, mientras que los resistores las tienen en fase, ¿cómo combinar todo esto para obtener los efectos finales en el comportamiento de este circuito?
El efecto conjunto se denomina "impedancia" y se puede decir que corresponde de manera simplificada a la "resistencia" que un circuito presenta a una corriente alterna. Por supuesto, la impedancia, aunque medida en ohm, no representa sólo una simple oposición al paso de la corriente, porque tiene en cuenta los efectos sobre la fase de la corriente en relación a la tensión.
Un ejemplo de cómo la impedancia puede ser calculada se da inicialmente combinando un resistor y un capacitor, como el lector puede ver en la figura 23.
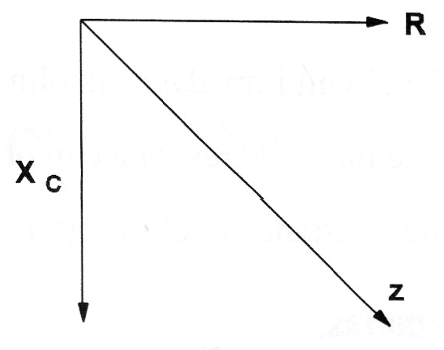
El resistor presenta una resistencia pura (óhmica) mientras que el capacitor tiene una reactancia capacitiva. Los dos tienen diferentes efectos sobre el circuito que, colocado en un gráfico, se desplazan de 90 grados unos de otros.
Esto significa que el resultado de los efectos es una suma vectorial, es decir, una suma que toma en cuenta la dirección y dirección de los efectos en el gráfico.
Así, llamando a la impedancia de Z, la resistencia de R y la reactancia capacitiva de C en este circuito, calculamos Z por la fórmula siguiente:
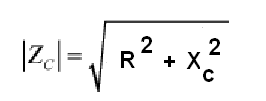
Donde:
Z es la impedancia (en ohms)
R es la resistencia (en ohms)
Xc es la reactancia capacitiva (en ohms)
También podemos tomar el caso de un circuito formado por un inductor y una resistencia, como se muestra en la figura 24.
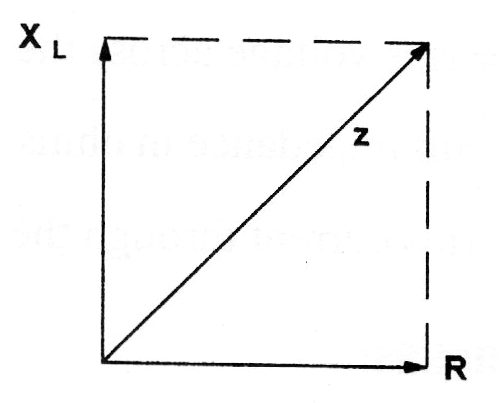
En este caso, la reactancia inductiva será representada diferentemente, como podemos ver en la misma figura la impedancia resultante.
Llamando de Z a la impedancia, R a la resistencia y XL a la reactancia inductiva, podemos calcular la impedancia por la fórmula abajo:
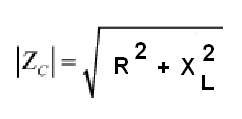
Donde:
Z es la impedancia (en ohms)
R es la resistencia (en ohms)
XL es la reactancia inductiva (en ohms)
Finalmente, tenemos el caso donde el circuito está formado por un resistor, un inductor y un capacitor como se puede ver en la figura 25.
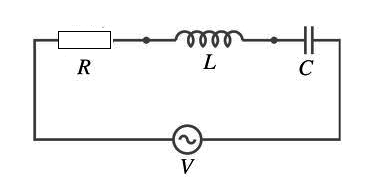
Se trata de un circuito RLC en el que se colocan los efectos de reactancias y resistencias en la forma gráfica como se muestra en la figura 26.
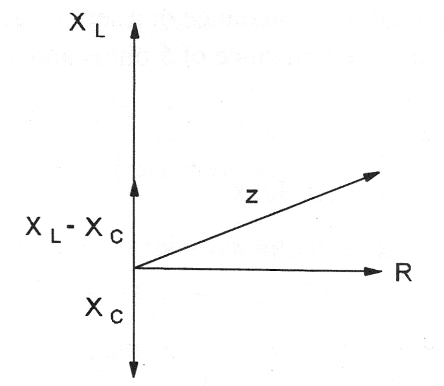
La impedancia de este circuito puede calcularse mediante la siguiente fórmula:
Donde:
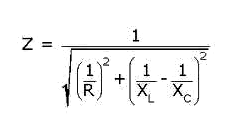
Z es impedancia (en ohms)
R es la resistencia (en ohms)
XC es la reactancia capacitiva (en ohms)
XL es la reactancia inductiva (en ohms)
Nótese que la suma de la reactancia capacitiva con inductiva es una suma vectorial, es, que se debe considerar como los signos de las magnitudes.
Múltiplos y Submúltiplos de Unidades de Energía, Corriente y Tensión
Para las unidades de corriente, tensión y potencia que estamos usando es común utilizar múltiplos y submúltiplos para expresar o valores muy grandes o muy pequeños.
A continuación, le damos los múltiplos y submúltiplos más comúnmente usados:
a) CORRIENTE
Unidad: ampère (equivalente a pasar una carga de 1 Coulomb por segundo por un punto de un conductor)
Abreviatura: A
Submúltiplos más comunmente usados:
1 miliampère (mA) = 0,001 A o 1 milésimo de ampère
1 microampère (uA) = 0,000 001 A o 1 milionésimo de ampère
1 nanoampère (nA) = 0,000 000 001 A o 1 bilionésimo de ampère
1 picoampère (pA) = 0,000 000 000 001 A o 1 trilionésimo de ampère
b) TENSIÓN
Unidad: Volt (equivalente a la tensión aplicada a un conductor de resistencia de 1 Ohm hace una corriente de 1 ampère)
Abreviatura: V
Múltiplos y submúltiplos:
1 microvolt (uV) = 0,000 001 V o 1 milionésimo de volt
1 milivolt (mV) = 0,001 V o 1 milésimo de volt
1 quilovolt (kV) = 1 000 V
1 megavolt (MV) = 1 000 000 V
c) POTENCIA
Unidad: watt (iguala a la producción de 1 joule por segundo)
Abreviatura: W
Múltiplos y submúltiplos:
1 picowatt (pW) = 0,000 000 000 001 W o 1 trilionésimo de watt
1 nanowatt (nW) = 0,000 000 001 W o 1 bilionésimo de watt
1 microwatt (uW) = 0,000 001 W o 1 milionésimo de watt
1 miliwatt (mW) = 0,001 W o 1 milésimo de watt
1 quilowatt (kW) = 1 000 W
1 Megawatt (MW) = 1 000 000 W
1 Gigawatt (GW) = 1 000 000 000 W
Unidades del SI
En el sistema internacional de unidades, las unidades básicas son:
| Grandeza Básica | Nombre | Símbolo | |
| Longitud | metro | m | |
| Masa | Kg | Kg | |
| Corriente eléctrica | Ampere | A | |
| Tiempo | Segundo | s | |
| Temperatura termodinámica | Kelvin | K | |
| Cantidad de sustancia | mol | mol | |
| Intensidad de la luz | Vela | CD |
Unidades derivadas del SI
=
| Grandeza derivada | Nombre | Símbolo |
| Área | Metro cuadrado | m2 |
| Volumen | metro cúbico | m3 |
| Velocidad | metro por segundo | m |
| Aceleración | Metro por segundo al cuadrado |
m2 |
| Número de onda | metro recíproco |
m-1 |
| Densidad de masa | Kilogramo por metro cúbico | kg/m3 |
| Volumen específico | Metro cúbico por kilogramo | m3/kg |
| Densidad actual | Amperio por metro cuadrado | A/m2 |
| intensidad del campo magnético | Ampere por metro |
A/m |
| Concentración de la sustancia | mol por metro cúbico | mol/m3 |
| Luminancia | Candelas por metro cuadrado | CD/m2 |
| Fracción de masa | Kilogramo por kilogramo (*) | 1 |
(*) Debe ser representantes por el número 1
Otras unidades fuera del SI
(aceptado para su uso con SI)
| Nombre | Valor en unidades si | Símbolo |
| Milla náutica | 1852 m | - |
| Nudos | 1 milla náutica por hora = 1852/3600 m/s | - |
| Bar | 1 barra = 1 MPa = 100 kPa = 1000 PA | bar |
| Are | 1 a = 100 m2 | a |
| hectáre | 1 ha = 10.000 m2 | Ha |
| Angstrom | 1 a = 0.1 Nm = 10-10m | A |
| Barn | 1 b = 100 FM2 = 10-28 m2 | b |
| Curie | 1 CI = 3.7 x 1010 BQ | Hay |
| Röentgen | 1 R = 2,58 x 10-4 C/kg | R |
| Radiano | 1 RAD = 1 cGy = 10-2 GY | Línea |
| Rem | 1 REM = 1 CSV = 10-2 SV | Rem |
| square mil | 1 sq mil = 645,2 µm2 | sq mil |
| Minuto | 1 min = 60 s | min |
| Hora | 1 hora = 60 min = 3600 s | h |
| grados (ángulo) | 1En = π/180 RAD | o |
| minuto (ángulo) | 1 ' = 1/60° | ‘ |
| segundo (ángulo) | 1 "= 1/60" | “ |
| Litro | 1 = dm3 | l |
| Neper | 1 NP = 1 | e.g. |
| bel | 1 B = ½ en 10 NP | B |
| Unidad astronómica | 1 UA = 1.495 98 x 1011 | UA |
Contenido
Parte 1 - Unidades - Energía (CUR2001S)
Parte 3 - Transistores de potencia bipolares (CUR2003S)
Parte 4 - MOSFETs de Potencia (CUR2004S)
Parte 5 - Los IGBTs (CUR2005S)
Parte 6 - Tiristores – El SCR (CUR2006S)
Parte 7 - Tiristores - El Triac (CUR2007S)
Parte 8 – Tiristores – Otros Dispositivos (CUR2008S)



