7.1 Qué son los osciladores
Sonidos se producen cuando una corriente eléctrica, que constantemente cambia de dirección, o aún sufre variaciones periódicas de intensidad, que circula a través de un transductor adecuado.
Cómo, por ejemplo, podemos mencionar a la cápsula de un auricular o altavoz. Para tener sonidos audibles, la frecuencia de esta corriente debe ser entre unos 15 y 15 000 Hz, pero como hay animales que pueden realizar las frecuencias más altas, el espectro de audio no sólo está limitado por estos valores.
En electrónica las frecuencias de la banda de audio son las que van hasta aproximadamente de 100 000 Hz, como el lector puede ver en la figura 1.
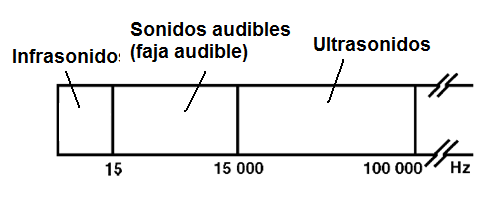
Por otro lado, para tengamos las ondas de radio o las ondas electromagnéticas, las corrientes también variables deben tener frecuencias que pueden ir desde unas pocas decenas de quilohertz, o incluso inferior, a miles de millones de hertz, siendo aplicadas a una antena. Las frecuencias en esta gama forman el espectro de radiofrecuencia o RF, como se muestra en la figura 2.
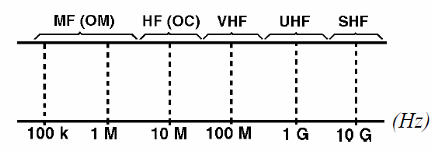
Para producir corrientes eléctricas de frecuencias que coinciden tanto con las frecuencias de la banda de audio (AF), como las que se utilizan los circuitos de radio frecuencia (RF), son usados circuitos que se denominan osciladores.
Básicamente, un oscilador no es más que un amplificador que está conectado de tal manera que, en su salida tengamos una señal con frecuencia y amplitud definidas.
Las propiedades eléctricas de los transistores bipolares permiten estos componentes a utilizarse en varios tipos de osciladores. La forma en que cada tipo de oscilador funciona, caracteriza su tipo y hay muchos de ellos, de los cuales veremos los principales en esta lección.
Para que un transistor oscile, la técnica utilizada es muy sencilla: podemos tomar la señal amplificada a la salida de un transistor utilizado como amplificador y aplicamos parte a su entrada, es decir, hacemos un circuito con retroalimentación positiva.
La señal de salida vuelve a la entrada y otra vez se amplifica, resultando en una nueva señal de salida que vuelve hacia la entrada, en un ciclo que dura indefinidamente (mientras que el circuito es alimentado), produciendo las oscilaciones, como el lector verá en figura 3.
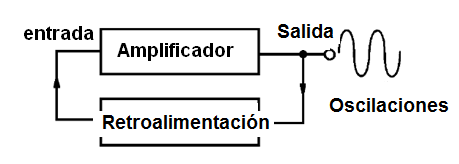
Tenemos un ejemplo de cómo funciona cuando conectamos a un amplificador con un micrófono conectado a la entrada y abrir el volumen. La señal del altavoz es recogida por el micrófono, pasando otra vez por el amplificador, en un ciclo que produce un fuerte silbido, o realimentación acústica. Este silbato es llamado "regeneración".
La velocidad a la que se aplica la señal a la entrada determina el tiempo de camino de la señal en un ciclo completo y, por lo tanto, la frecuencia de funcionamiento del oscilador.
Vea que es de fundamental importancia que la "ganancia" del amplificador sea mayor que 1, es decir, la señal de salida debe ser "más fuerte" que el de la entrada.
Si tenemos un circuito con ganancia menor que 1, la señal de salida será más débil que la entrada y ya no será capaz de excitar el circuito con la misma intensidad en el ciclo siguiente, lo que debilita un poco más.
El nuevo ciclo aún más débil sólo conduce a una salida aún más baja. Esto significa que la señal generada se reducirá luego en intensidad, dando lugar a lo que llamamos "oscilación amortiguada" para desaparecer, como podemos ver en la figura 4.
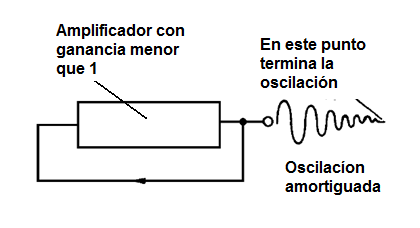
Está claro que un circuito con ganancia exactamente de una vez no es conveniente para el uso práctico, porque no podemos "tomar" cualquier porción de la señal para uso externo. Si hecho esto, tendremos una señal más débil en la entrada y las oscilaciones amortecen.
Para que podamos usar la señal generada, la ganancia debe ser mayor que uno, para que "sobre" una buena parte de la señal para uso externo.
Otra condición importante para usar un oscilador es que la señal aplicada a la entrada tenga la fase correcta. No basta conectar simplemente a la salida (colector) de un transistor en configuración de emisor común en la entrada (base), como el lector puede ver en la figura 5, para que el circuito entre en oscilación.
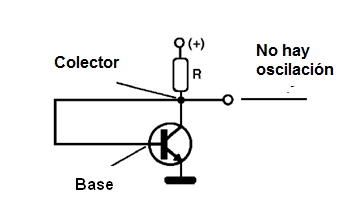
Como hemos estudiado en lecciones anteriores en esta configuración que el transistor invierte la fase de la señal, lo que significa que, para el circuito, la señal en la entrada no causa refuerzo se vuelve a aplicar, sino debilitar el proceso, y no hay ninguna oscilación.
En un circuito como este, para haber oscilación cuando se vuelva a aplicar la señal a la entrada, es necesario interponer cualquier sistema para invertir la fase de la señal. Vea figura 6 para tener cómo debe hacerse.
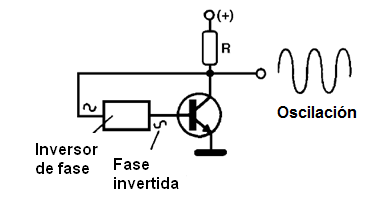
El sistema que invierte la etapa de la señal también es responsable por un retraso. Este retraso puede ser calculado para que sea un ciclo de la señal y con eso determinar la frecuencia de la señal generado.
Las redes de retroalimentación, como se les llama, pueden ser de varios tipos, habiendo cálculos que permiten calcular la frecuencia de su operación.
El tipo de señal generada, es decir, su forma de onda también depende de la forma en que se realiza la retroalimentación. Como veremos, para estudiar los distintos tipos de osciladores, las señales generados pueden tener muchas formas diferentes, siendo el más común los que tienen curvas de seno, triangulares, diente de sierra y triangulares.
Y también, como veremos a continuación, los distintos tipos de osciladores según la forma de la señal que es tomada de la salida y aplicada en la entrada, así como los cambios de etapa ocurren cuando es necesario. También se verá que todos los osciladores tienen sus limitaciones, que hace aplicable en ciertas bandas de frecuencia y aplicaciones.
7.2 – Oscilador Hartley
Se trata de un tipo de oscilador LC, es decir, en el que se determina la frecuencia de la señal producida por un inductor y un capacitor. Vea la figura 7 la configuración básica de este oscilador, observando que la bobina tiene una salida o derivación.
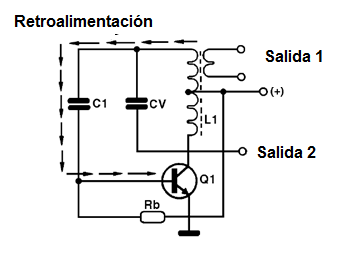
El resistor Rb, hace la polarización de la base del transistor y el capacitor C1 el circuito de retroalimentación, es decir, "juega" parte de la señal de la salida a la entrada del circuito. El funcionamiento de este oscilador es el siguiente:
Cuando encienda el circuito, la resistencia polariza la base del transistor cerca de la saturación, pasando entonces a su conducción. Una fuerte corriente pasa entre el colector y la fuente de alimentación, conectado a la bobina central L1.
El resultado es que esta corriente en L1 induce a la otra mitad de la misma bobina una corriente que se aplica a la base del transistor, a través del capacitor C1. El sentido del movimiento de esta corriente es tal que el transistor es conducido casi al corte. Como resultado, cae la corriente de colector y por lo tanto en L1, con un efecto que reduce la inducción de la corriente en la otra mitad de la bobina del mismo y, por tanto, a través de C1 y la base del transistor.
Con eso, otra vez tenemos el predominio de la polarización por el resistor, que hace que el transistor conduce y comience un nuevo ciclo. El transistor es entonces en este "ida y vuelta" entre la corte y la saturación, produciendo una señal cuya frecuencia está determinada por la bobina y el capacitor en paralelo, puesto que la inducción que vimos también tiene en cuenta la carga y descarga del capacitor CV.
Esta señal del oscilador puede ser tomada tanto del colector del transistor como una bobina adicional sobre L1. Puede utilizarse este tipo de oscilador para producir señales y frecuencias que van desde unos pocos Hertz (audio) hasta unas decenas de MHz (RF). La principal limitación que hemos encontrado para este tipo de oscilador cuando se trabaja en la banda de audio, es que necesitamos bobinas de alta inductancia.
Fórmula Para la Frecuencia del Oscilador Hartley
En un oscilador Hartley, que el lazo de retroalimentación es hecho por la bobina de carga L este circuito trabaja hasta unas pocas decenas de Mega Hertz. La frecuencia de un oscilador Hartley es dada por el circuito LC resonante como se muestra en la figura 8.
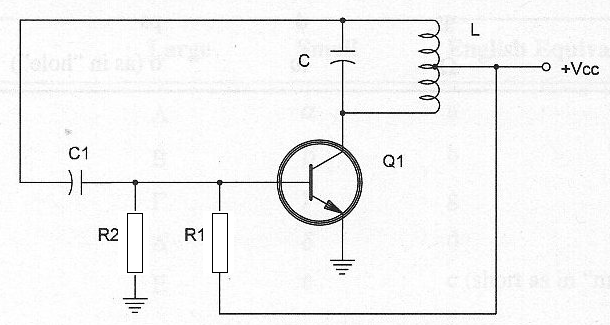
f
1
2 x π x √(L x C)
Donde:
F es la frecuencia en Hertz (Hz)
L es la inductancia en Henry (H)
C es la capacitancia en faradios (F)
π es 3.1416
7.3 - OSCILADOR DE COLPITTS
El oscilador de Colpitts, tiene un principio de funcionamiento similar a la del oscilador Hartley, con la única diferencia que la señal de la retroalimentación positiva se obtiene en una derivación basada en capacitores, como se muestra en la figura 9.
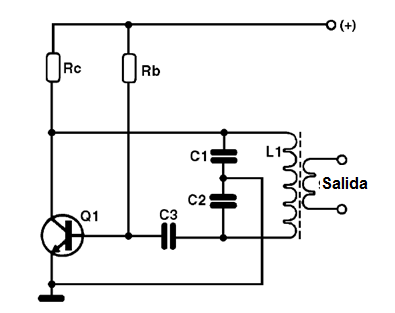
El transistor permanece en conducción durante los semiciclos positivos de la señal y va próximo al corte en los semiciclos negativos. Vea que la frecuencia está dada por la bobina L1 y el capacitor en paralelo.
Este circuito opera en un rango de frecuencias de unos pocos hertz a unas decenas de megahertz.
Observamos que, para el caso de los transistores en el oscilador Hartley, como Colpitts, así como otros componentes de semiconductores, es posible construir una configuración equivalente con válvulas. La señal generada por este circuito puede ser retirada desde el colector del transistor, como a partir de una bobina, formando un secundario del transformador, como el lector puede en la imagen 10.
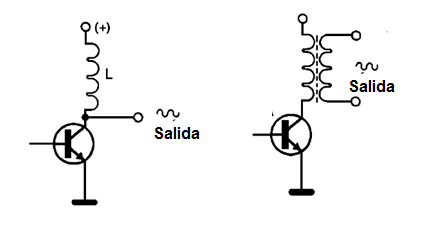
Oscilador de Colpitts
En el oscilador de Colpitts o simplemente Colpitts, la retroalimentación es hecha por un divisor capacitivo, como se muestra en la figura 11. La frecuencia también depende el circuito LC, y suele ser la fórmula para el cálculo se expone a continuación.
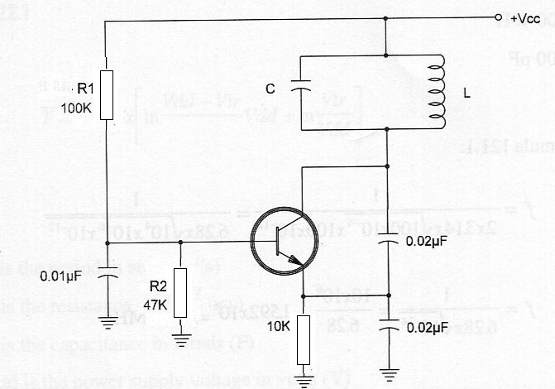
Fórmula
f
1
2 x π x √(L x C)
Donde:
f es la frecuencia en Hertz (Hz)
π es la constante 3.1416
C es la capacitancia en Farads (F)
L es la inductancia en Henry (H)
7.4 - OSCILADOR DE BLOQUEO
Una configuración bastante importante utilizada como oscilador con transistores bipolares puede verse en la figura 12. Consiste en un oscilador de bloqueo, con un transistor en configuración de emisor común.
Vea lo que le estamos dando ejemplos de configuración que hacen uso de transistores. Sin embargo, las configuraciones, son equivalentes con las válvulas y otros componentes.
El colector del transistor está conectado a la bobina primaria de un transformador cuyo secundario se corresponde con el circuito de retroalimentación. El secundario está conectado a la base del transistor. El transistor se polariza cerca del punto de saturación pela conexión del resistor Rb.
Cuando alimentamos el circuito, el resistora polariza la base del transistor para conducir, produciendo un pulso de corriente en el primario del transformador (L1).
Esto induce una corriente en el secundario que se opone a la polarización de Rb y conduce el transistor al corte. Con eso el transistor "se apaga" y otra vez entra en acción la polarización del resistor causando otra vez la producción de un pulso en el colector. El capacitor C1 controla tanto la corriente de polarización, cargándose con ella, como opuesto, descarga y con eso determinando la frecuencia de operación junto con C.
La frecuencia de operación está determinada también por la inductancia de la bobina y el capacitor en paralelo. Tenga en cuenta que este circuito debe "disparado" por un impulso externo, pero hay versiones que son "self shot", es decir, entra en funcionamiento cuando se establece la alimentación.
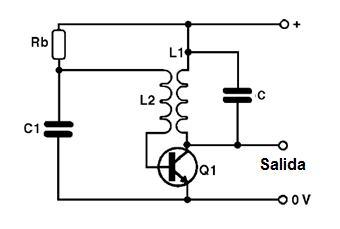
Las versiones que deben activarse externamente son ampliamente utilizadas en televisores, en circuitos de sincronismo en que una señal externa controla el oscilador, que es responsable de mantener la estabilidad de la imagen. Puede hacer el mismo circuito con un transistor conectado en la configuración de base común, como se muestra en la figura 13.
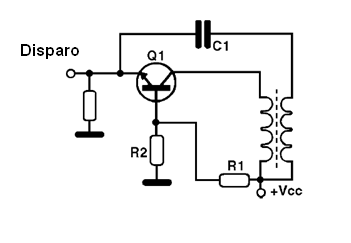
Vea para que la señal se retira del colector y re-aplicado al emisor del transistor, con una polarización fija en la placa del transistor. El pulso se aplica a la base. Estos circuitos pueden utilizarse a frecuencias que van desde unos pocos hertz a unas decenas de megahertz. En la figura 14 tienen la típica forma de onda producida por un oscilador de este tipo.
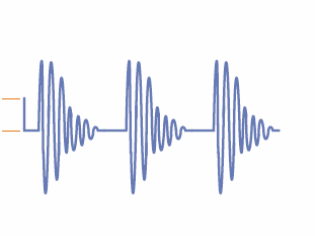
La frecuencia de este circuito se calcula del mismo modo que los circuitos anteriores, en el circuito resonante LC en el colector del transistor.
7.5 - OSCILADOR DE DOBLE T
El nombre de este oscilador es debido a la red retroalimentación que proporciona una inversión de la señal de base usando solamente resistores y capacitores, como el lector puede ver en figura 15.
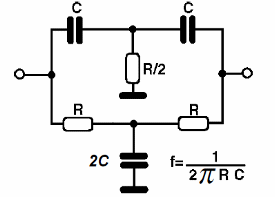
Para que el T doble funcione, proporcionando la inversión de fase deseada, los componentes que forman deben mantener los valores en una relación bien definida.
Así:
R1 = R2 = 2 x R3
C1 = C2 = C3/2
La frecuencia de funcionamiento del oscilador es dada por la fórmula:
f
1
2 x π x RC
Donde
R = R1 = R2 - la resistencia en ohms (ohms)
C = C1 = C2 -Capacitancia en farads
π = 3.14 (constante)
f = frecuencia en Hz
En la figura 16, tenemos un oscilador de doble T completo, con un transistor en configuración de emisor común.
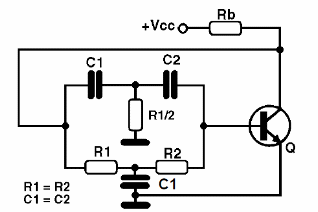
Los capacitores deben seleccionarse según la frecuencia de operación deseada. Podemos cambiar ligeramente la frecuencia del oscilador y conseguir incluso oscilaciones amortiguadas mediante un potenciómetro de ajuste o el potenciómetro R3 como se muestra en figura 17.
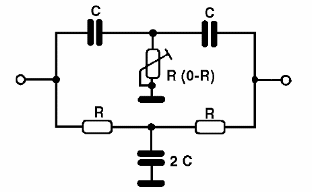
En la figura 18 tenemos las oscilaciones amortiguadas producidas por un oscilador de este tipo.
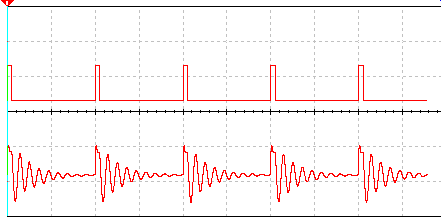
Este oscilador se presta principalmente a la producción de señales en la banda de audio. Es importante tener en cuenta que las formas de onda de las señales del oscilador dependen mucho de la configuración.
Generalmente busca generar señales sinusoidales en todas las versiones que vimos, pero dependiendo de las características de los componentes utilizados, pueden ocurrir deformaciones. En el caso de oscilador de doble T la señal es sinusoidal.
7.6 - Oscilador por desplazamiento de fase
En este tipo de oscilador, contamos con una red de resistores y capacitores que forman el circuito de retroalimentación, cambiando en 180 grados la fase de la señal. De esta manera, tenemos la inversión de la fase necesaria al mantenimiento de las oscilaciones. Vea la figura 19, donde tenemos un circuito de oscilador de desplazamiento de fase con un transistor.
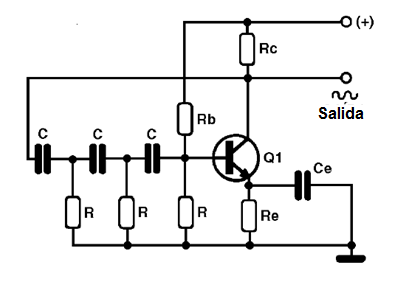
La frecuencia de operación de este oscilador es dada por la fórmula:
f
1
2 x π x √(6RC)
Donde:
f es la frecuencia de operación en Hertz
π es constante, valiendo 3.14
R es el valor de las resistencias utilizadas en células en ohms
C es el valor de los capacitores utilizados en células en farads.
En este circuito, cada resistor, conjuntamente con un capacitor, cambia de en 60 grados de la fase de la señal, por lo que, con 3 celdas, tiene 180 grados en la fase de la señal, es decir, obtenemos su inversión.
Para los lectores no familiarizados con esta forma de especificación de la fase de hacemos una observación: lo que pasa es que un ciclo completo de una señal corresponde a un giro completo de un generador "imaginario" que, como el lector puede ver en la imagen 20. (Vea el volumen anterior Electrónica Básica).
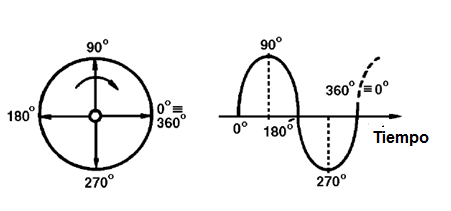
Por lo tanto, una vuelta completa del generador, es decir, un ciclo completo corresponde a 360 grados. Cuando las dos señales están en el mismo punto "imaginario", es decir, un ciclo, decimos que están en fase.
Si la diferencia en la posición de estas señales es tal que nos 1/4 vuelta, o 90 grados, como se muestra en la figura 21, decimos que estas señales están en cuadratura.
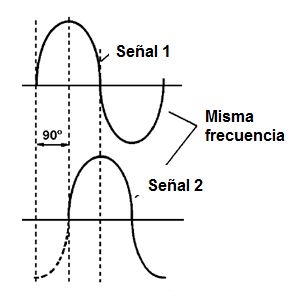
Por otro lado, si la diferencia de puntos es tal que ha media vuelta, es decir, 180 grados, lo que significa que, cuando uno está a lo más positivo la otra será más negativa, decimos que estas señales están en oposición de fase o con las fases invertidas como el lector puede comprobar en la figura 22.
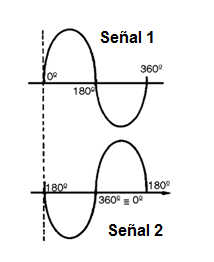
Los osciladores de desplazamiento de fase son utilizados sólo para producir las señales de frecuencias en la banda de audio.
Ejemplo de aplicación:
Determine la frecuencia de operación del circuito de oscilador en figura 23.
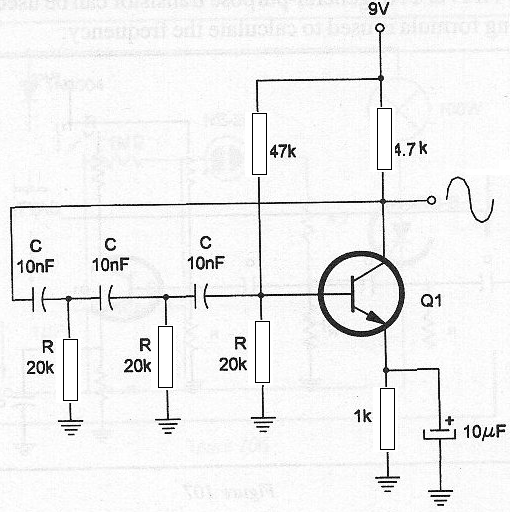
Datos:
C = 10 nF = 0.01 μF
R = 20 kohms
f = ?
Aplicando la fórmula:
f
1
4.88 x 3.14 x 20 x 103 x 0.01 x 10-6
f
103
3.06
f
326.8 Hz
7.7 - MULTIVIBRADOR ASTABLE
Llegamos ahora a una configuración que produce señales de modo especial porque además de las señales tienen una forma de onda rectangular son dos los transistores usados. En la figura 24 tenemos la configuración básica de un multivibrador astable con dos transistores NPN. Esta misma configuración puede obtenerse con transistores PNP, los transistores de efecto de campo, válvulas y otros componentes activos.
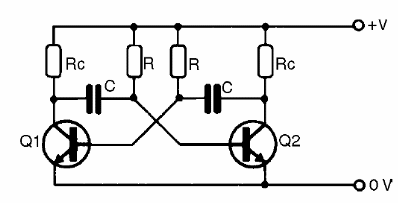
Los dos transistores se conectan de tal manera que, en cada momento, cuando uno está en el corte lo otro va estar saturado, que es, sólo uno de los transistores puede conducir a la vez. Podemos comparar este circuito a un balancín que, cuando uno "hasta" el otro lado necesariamente "hacia abajo", como indica la figura 25.
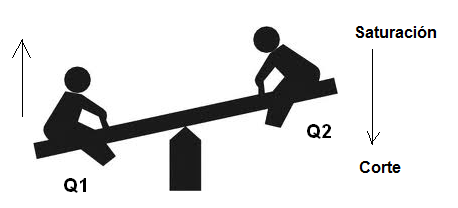
En el multivibrador astable, como su nombre indica, la conducción de los transistores no es una situación estable, para que cada transistor solo puede estar por un tiempo limitado en esta condición.
Esto hace que los dos transistores en el circuito queden cambiando constantemente de estado, pasando del corte a la saturación y viceversa, a una velocidad que depende de los componentes utilizados, como el lector puede ver la figura 26.
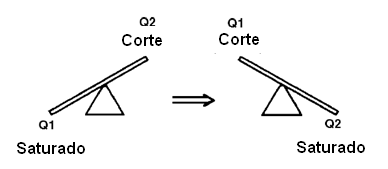
Basado en el circuito de la figura, vamos a ver cómo funciona: mediante el establecimiento de la alimentación los transistores están polarizados de modo que vayan a la saturación por los resistores de base. Sin embargo, debido a diferencias en características, uno de ellos conduce más que el otro y luego se satura. Con eso, el otro transistor se impide conducir y permanece en el corte.
Suponiendo que Q1 ir a saturación y Q2 volver a la corte, el capacitor C1 comienza a cargar a través del resistor R1 hasta el momento en que alcanza una tensión suficiente para polarizar Q2 para hacerlo conducir. Cuando esto ocurre el circuito conmuta y Q1 pasa a la corte mientras que Q2 será llevado a la saturación.
Es en este punto, es C2 que empieza a descargar a través de R2 hasta que el transistor Q1 sea llevado a la conducción. El circuito quedara cambiando de estado indefinidamente (en cuanto haya alimentación), a una velocidad que depende de los valores de los capacitores y resistores utilizados.
Como la conmutación de los transistores ocurre muy rápidamente, la señal producida tiene forma de onda rectangular. Vea que se puede retirar la señal del circuito tanto del colector de Q1, como colector de Q2.
Sin embargo, estas señales serán de diferentes niveles. Así, en momentos en que la tensión de colector de Q1 está cerca del positivo de fuente de alimentación (corte), es decir, que tenemos un nivel alto de tensión en el colector, Q2 estará en cero (saturación), y tenemos un nivel bajo de tensión.
Decimos que las salidas son complementarias y se representan por Q y Q\. La barra en la Q indica la situación complementaria. Si los capacitores y resistores utilizados son el mismo, el tiempo de conducción y corte de cada transistor va a ser el mismo, y entonces tendremos una señal "cuadrada", es decir, con tiempos de nivel alto y bajo iguales, como el lector puede ver en la figura 27.
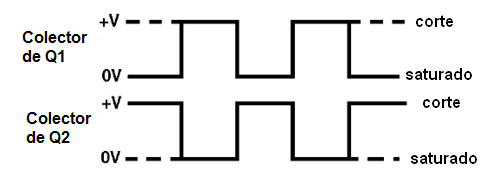
La frecuencia de un multivibrador astable será mayor cuanto más pequeños sean los capacitores utilizados. En la práctica, con los transistores comunes, el límite superior para la frecuencia de operación de este circuito es alrededor de 5 MHz. Sin embargo, con los transistores muy rápidos, usted puede conseguir frecuencias llegan a 100 MHz.
En la figura 28 tenemos la versión del multivibrador astable con transistores PNP, observándose que se invierten sólo los sentidos de circulación de las corrientes.
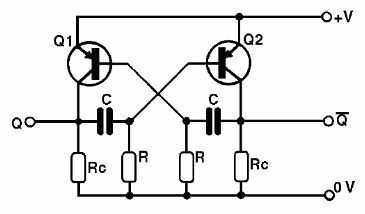
Los multivibradores astable son ampliamente utilizados en circuitos de lógica que, como ya explicado, admiten dos niveles de tensiones solamente. Ellos funcionan como relojes o "clocks" (relojes), determinando el ritmo o la velocidad de su operación.
Ciclo Activo
Durante un determinado período, la señal rectangular permanezca en el nivel alto, junto con el tiempo que permanece en nivel bajo resultan el período total. Sin embargo, las señales pueden ser asimétricas en relación con esos dos tiempos. Cuando el tiempo en el nivel alto es igual al tiempo de bajo nivel, como se muestra en la figura 29, decimos que es un "cuadrado", aunque este nombre no es muy elaborado en el sentido de que las unidades en el sentido vertical son amplitudes y en el sentido horizontal son tiempos
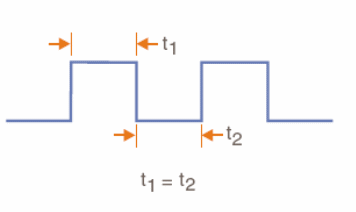
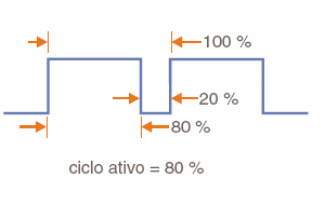
Para las señales en que los tiempos en nivel bajo y alto son diferentes, podemos hablar del ciclo activo como el porcentaje del tiempo total del ciclo en el cual la señal permanece en alto nivel, como se muestra en la figura 30.
Cálculo de la frecuencia del multivibrador Astable
Para el circuito de la figura 31, podemos calcular la frecuencia por fórmulas que se indican a continuación.
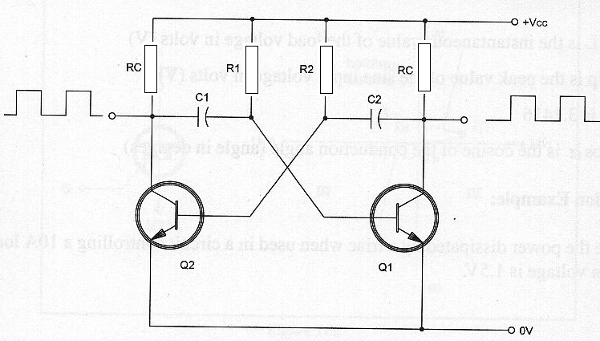
Formula:
Tiempo de conducción
tp
0.69 x R x C
Donde:
tp es el tiempo de conducción del transistor en segundos (s)
R es la resistencia en ohms( ohms)
C es la capacitancia en Farads (F)
Fórmula:
Frecuencia
f
1
tp1 + tp2
f
1
0.69 x (R1 x C1 + R2 x C2)
Donde:
f es la frecuencia en Hertz (Hz)
R1, R2 es la resistencia en ohms (ohms)
C1, C2 son las capacitancias en farads (F)
Fórmulas derivadas:
Fórmula
Oscilador cuadrado (50% de ciclo activo) - R1 = R2 = R y C1 = C2 = C
f
1
1.38 x R x C
Donde:
f es la frecuencia en Hertz (Hz)
R es la resistencia en ohms(ohms)
C es la capacitancia en farads (F)
Fórmula
Frecuencia como una función de C cuando R1 = R2 = R y C1 = C2 = C.
f
1
2 x tp
Donde:
f es la frecuencia en Hertz (Hz)
Tp es el tiempo de conducción en segundos (s)
Ejemplo de aplicación:
Determine la frecuencia del multivibrador astable que se muestra en la figura 32.
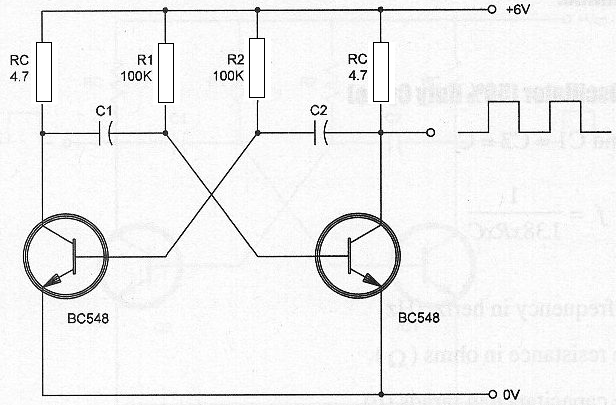
7.8 - Armónicos
Abrimos un pequeño paréntesis en este punto del curso, para tratar de este tema que está relacionado con las formas de onda producidas por osciladores. Un matemático francés llamado a Fourier, en el siglo XIX, demostró mediante cálculos, que podríamos conseguir cualquier forma de función periódica para la combinación simple de la forma correcta de una forma única que es la senoidal.
De esta manera, incluso una señal rectangular (que puede ser descrita por funciones periódicas) puede ser "sintetizada" simplemente usando una onda sinusoidal, que son las formas "puras" o fundamentales de onda como se muestra en la figura 33.
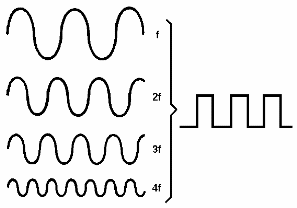
Entonces, qué es la onda de frecuencia que generamos, es decir, lo fundamental, se combinan con unas frecuencias de onda que son múltiples, es decir, doble, triple, cuádruple, etc., de esta frecuencia fundamental. Estas frecuencias múltiples se llaman "armónicos", como el lector puede ver en la figura 34.
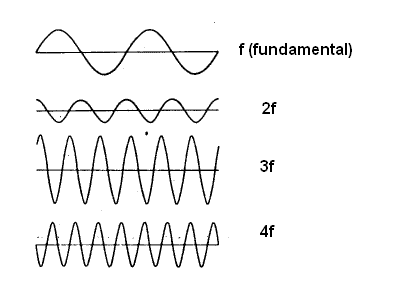
Lo interesante en electrónica es que cuando tenemos una señal o una forma de onda compleja (no sólo seno), ella se comporta como realmente teniendo una frecuencia fundamental y armónicos de intensidad, disminuyendo a medida que aumenta la frecuencia y ¡Esto hasta el infinito!
Así, en el caso de un multivibrador astable, que es una forma de oscilador que genera una señal particularmente rico en armónicos, incluso operando a bajas frecuencias y sus armónicos extiende de alta frecuencia y así también puede ser utilizado en aplicaciones prácticas.
Un oscilador de este tipo operando en sólo 1 kHz, por ejemplo, tienen suficientes armónicos en 1 MHz para excitar un transistor de radio y así utilizarse como un inyector de la señal.
7.9 - OSCILADOR DE RELAJACIÓN
Existen componentes que son más apropiados que los transistores normales para el proyecto de los llamados osciladores de relajación, pero es interesante también estudiar este tipo de aplicación, ya que servirá como una buena base para las próximas lecciones. En la figura 35, para ver el circuito básico de un oscilador de relajación con dos transistores.
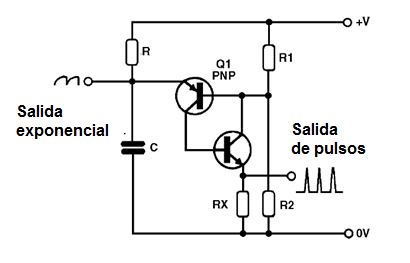
Los dos transistores están conectados para formar una llave, es decir, un circuito regenerativo que se alimenta a sí mismo.
Conectamos así en la entrada de este transistor una red RC de tiempo y polarizamos la otra de modo constante, con un divisor de dos resistores. El transistor PNP tiene su base polarizada para dejarlo cerca de la plena conducción.
Cuando la tensión en el capacitor aumenta, a medida que se carga a través del resistor R, el transistor PNP aumenta su conducción y la base de los transistores NPN se polariza para también hacerle aumentar su conducción.
El resultado del aumento de la corriente base del transistor NPN es una mayor polarización de base del transistor PNP, en un proceso de retroalimentación: la más grande la tensión de base del PNP tensión causa un incremento de la corriente del NPN.
A partir de este momento cuando el capacitor se descarga, luego hay un momento en que la tensión en las armaduras hace que este proceso de retroalimentación se produce rápidamente, llevando los dos transistores a la saturación.
Llegamos entonces al punto donde el capacitor está cortocircuitado y descarga con un pulso de corriente. Después el pulso, los transistores se apagan y el capacitor empieza a cargar otra vez, hasta que fue nuevamente exitoso el nuevo punto de disparo.
El circuito entonces produce un "tren de pulsos cuya frecuencia depende de la velocidad de carga del capacitor a través del resistor de carga. En el capacitor, luego tenemos una onda exponencial, como el lector verá en la figura 36.
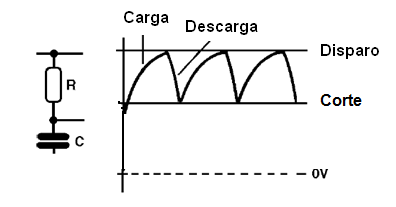
Este circuito se utiliza para generar relativamente señales de baja frecuencia, en la banda que va entre 0,01 Hz hasta 10.000 Hz o más.
Oscilador de Relajación con Lámpara de Neón
Un componente ampliamente utilizado en la construcción de los osciladores de la relajación es la lámpara de neón. Este componente presenta una característica de resistencia negativa, es decir, cuando la tensión aplicada alcanza cierto valor, el dispara y su resistencia cae.
La lámpara de neón puede utilizarse para producir señales diente de sierra en la gama de hasta unas decenas de quilohertz. El único inconveniente de este componente es que la tensión del disparo de una lámpara de neón es muy alta, del orden de 70 V o 80 V y la tensión en el cual ella se apaga, una vez que se activa es del orden de 50 V.
Sabemos que, en el circuito de RC, el capacitor se carga exponencialmente cuando aplicamos una tensión. Si conectamos una lámpara de neón en paralelo con él, cuando se alcanza la tensión de disparo, él conduce, descarga el capacitor hasta la tensión, cuando ella apaga.
Un nuevo ciclo de carga tiene entonces inicio, produciéndose una forma de onda diente de sierra.
La figura 37 muestra la configuración básica de un oscilador de relajación con una lámpara de neón. Este circuito es conveniente para la frecuencia fraccional de hertz hasta algunos quilohertz y opera con tensiones de 80 V.
Una lámpara de neón típica va enciende con 70 V. Si la tensión se reduce a algo alrededor de 50 V la lámpara se apaga y deja de conducir la corriente. La siguiente fórmula es válida para estos parámetros.
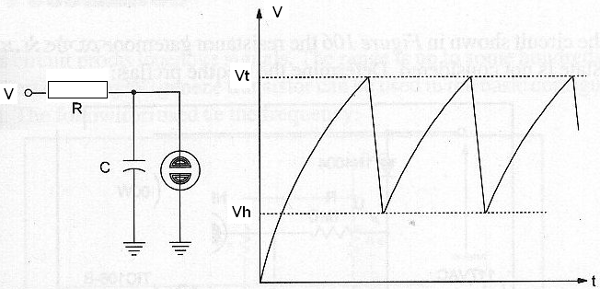
Fórmula
Período
T = R x C ln (
V - Vh
V - Vt
)
Donde:
T es el tiempo en segundos (s)
C es la capacitancia en Farads (F)
R es la resistencia en ohms (ohms)
V es la tensión en voltios (V)
Vt es la tensión de disparo en volts (V) -70 V typ.
Vh es la tensión manutención en volts (V) - 60 V typ.
Fórmula
Frecuencia:
f =
1
R x C x ln ( V – Vh / V – Vt )
Donde:
f es la frecuencia en Hertz (Hz)
C es la capacitancia en Farads (F)
V es la tensión en voltios (V)
Vt es la tensión de disparo en voltios (V)
Vh es el mantenimiento de tensión en voltios (V)
El procedimiento para el uso de la fórmula es la misma que en el oscilador de relajación con transistor de unijuntura, descrito en esta sección.
7.10 - OTROS OSCILADORES
Un interesante tipo de oscilador por su sencillez y su capacidad para excitar los puntos de salida con buena energía es lo que el lector puede ver en la figura 38.
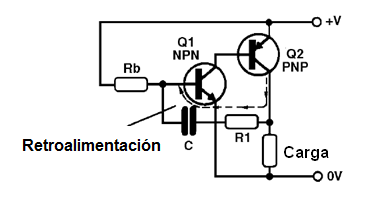
Este oscilador utiliza dos transistores complementarios, es decir, un NPN y PNP un formando un amplificador de acoplamiento directo. La señal de retroalimentación es responsable de las oscilaciones se hace quitando la señal directamente de la carga (colector del transistor PNP), y volver a aplicar a la base del transistor a través de un capacitor en serie con una resistor.
El resistor que polariza la base del primer transistor lo faz conducir y con él también el segundo transistor, que pronto tiene una elevación de la tensión del colector. Esta elevación causa la producción de un pulso de corriente a través del capacitor, y por un momento el transistor NPN (primero) cerca del corte.
Parando la conducción de este transistor dejando por un momento y con eso también el segundo, comienza un nuevo ciclo, con el primer resistor de base del primero transistor condiciendo. La frecuencia de operación de este oscilador está determinada entonces por el valor de resistor de polarización de base del primero transistor como por el valor del capacitor en el circuito de realimentación.
Otros osciladores importantes:
- Oscilador de Pierce
- Oscilador Puente de Wien
- Oscilador de Clapp
7.11 - Control de frecuencia
La frecuencia de un oscilador puede ser modificada con el uso de un elemento que afecta a esta grandeza y usted puede tener su valor cambiado externamente. Entonces podemos usar inductores, capacitores y resistores variables para este propósito.
En el caso de alta frecuencia osciladores como Hartley, Colpitts, tipo de bloqueo, podemos tener inductores con núcleos variables (ajustables) o entonces capacitores variables, dependiendo de la faja de frecuencias que queremos "barrer", como se muestra en la figura 39.
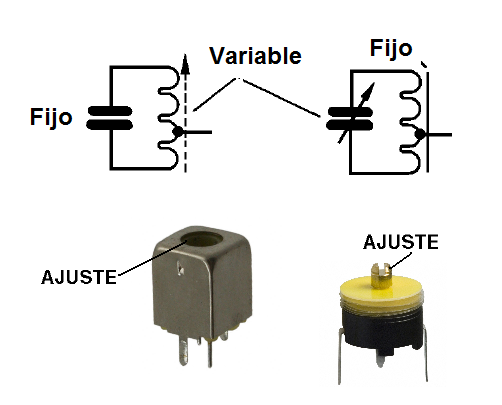
En el caso de osciladores de baja frecuencia, o de tipo RC, es común el uso de potenciómetros o trimpots, puesto que los capacitores que se utilizan generalmente son fijos, dado su alto valor. En la figura 40 tenemos la manera de variar la frecuencia de modo sensible, actuando en la polarización de un transistor en un oscilador Hartley.
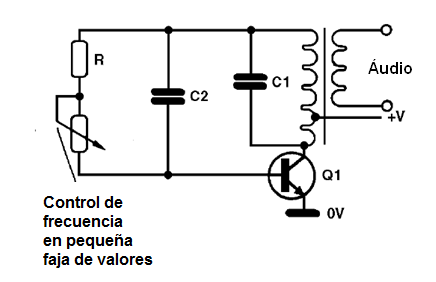
En la figura 41 el lector verá una forma de variar la frecuencia y también el ciclo activo en un multivibrador astable. Vea, en todos los casos utilizamos potenciómetros o trimpots, actuamos sobre la polarización, por lo que siempre debemos tener cuidado de mantener la banda de valores de la resistencia a presentada dentro de lo que el transistor admite para oscilación.
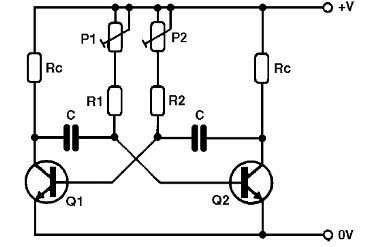
En el caso del oscilador Hartley, por ejemplo, puede haber " pistas muertas " en la cual las oscilaciones no se producen, el mismo que ocurre en relación con el multivibrador.
7.12 – Base común
Una característica de los osciladores de configuración de base común, es que los transistores tienen mucho menor capacitancia de entrada influyendo en la velocidad en la que puede funcionar. De esta manera, en esta configuración, podemos desarrollar fácilmente osciladores que alcanzan cientos de megahertz, como se aprecia en la figura 42.
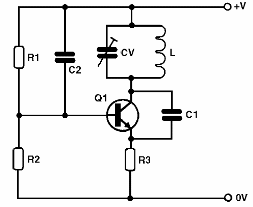
Esto oscilador tiene su frecuencia dada por el circuito LC, y la retroalimentación se obtiene "sacando" la señal del colector y lanzando al emisor del transistor del capacitor conectado entre estos dos elementos. Circuitos como este, son muy utilizados en transmisores de más de 20 MHz, receptores super-regenerativos y conversores.
Contenido
Lección 7 <--




