Los amplificadores operacionales pueden ser usados en una infinidad de proyectos, destacándose los de filtros activos, que adquieren características propias que difícilmente se pueden conseguir con otras bases. En especial, los amplificadores operacionales con transistores de efecto de campo en la entrada se prestan a la elaboración de innumerables tipos de filtros que encuentran aplicaciones en audio, instrumentación, instrumentos musicales, etc. En este artículo destacamos algunos tipos de filtros con operacionales, con su teoría básica y algunos circuitos prácticos. Las informaciones para la elaboración de este artículo provienen de manuales de fabricantes, como Texas Instruments, además de otras fuentes que se citarán al final del artículo.
¿Qué es un filtro? Partiendo de esta pregunta creemos estar atendiendo a una gran cantidad de lectores, principalmente los estudiantes, que necesitan una base mas firme para entender bien el asunto.
Podemos entonces definir un filtro como un circuito capaz de comportarse de manera selectiva ante señales de determinadas frecuencias. Los filtros pueden ser pasa-bajos, pasa-altos, o pasa-bandas, según dejen pasar las señales de frecuencias bajas, frecuencias altas, o de una banda determinada, según sugiere el nombre. Las "respuestas" de estos filtros representadas gráficamente son mostradas en la figura 1.

Vea que en (a), por ejemplo, tenemos un filtro pasa-bajos en que todas las señales por debajo de una determinada frecuencia, denominada "de corte", pasan sin sufrir atenuación, mientras que las demás son atenuadas en un grado que va a depender de la acción del circuito.
Los filtros básicos están formados solamente por componentes pasivos, tales como resistores, capacitores e inductores, de modo que las señales pasan sin sufrir ningún tipo de amplificación. Esto significa que los filtros de este tipo atenúan las señales de las frecuencias que no corresponden a aquella banda que deben dejar pasar; estos se denominan "filtros pasivos".
En la figura 2 tenemos algunos ejemplos de filtros de este tipo.

La atenuación, incluso de la seña que debería pasar sin sufrirla, hace que los filtros de este tipo encuentren muchas limitaciones en las aplicaciones prácticas.
La combinación de los elementos de un filtro de este tipo con amplificadores operacionales agrega a los filtros una propiedad importante: la de poder amplificar las seriales que correspondan a una banda deseada de frecuencia, o por lo menos evitar que ocurran perdidas en un nivel que impida su utilización práctica.
Esto nos lleva a filtros que presentan una ganancia real de potencia o amplificación, y que son denominados filtros activos.
En un filtro activo tenemos un amplificador que puede agregar energía al sistema, resultando al mismo tiempo un efecto de filtrado y una ganancia de potencia.
Los filtros de este tipo presentan otras ventajas como, por ejemplo, su baja impedancia de salida, la posibilidad de asociar diversas etapas sin perdidas de potencia y la capacidad de obtener funciones con alto Q en bajas frecuencias, sin necesidad de usar inductores.
En los circuitos de baja frecuencia esta posibilidad de no recurrir a inductores es importante, ya que estos componentes deberían tener valores altos, lo que tiene como resultado piezas caras y voluminosas.
Conforme el tipo de circuito, los filtros pueden proyectarse con características que van de 6 a 50dB por octava.
Dentro de las ventajas de estos circuitos destacamos las siguientes;
No hay pérdida por inserción. El sistema puede proporcionar ganancia, si es necesario.
Costo. Los componentes de los filtros activos son más baratos que inductores, principalmente los de valores elevados.
Sintonía. Los filtros activos pueden ser sintonizados fácilmente y ajustados en una amplia banda de frecuencias sin alteración de las curvas de respuesta.
Aislamiento. Estos filtros presentan buen aislamiento en vista de su elevada impedancia de entrada y baja impedancia de salida, lo que reduce a un valor mínimo la interacción entre el filtro y su carga.
Damos a continuación algunos tipos de filtros que tienen por base amplificadores operacionales.
Filtro pasa-banda
En este tipo de filtro tenemos el pasaje de señales de una banda específica de frecuencias, con el rechazo de señales de todas las otras frecuencias que no estén en esta banda.
El equivalente pasivo más común hace uso de un inductor y un capacitor (LC), pero en las bajas frecuencias el proyecto se vuelve difícil en vista de la necesidad de grandes inductores.
El circuito activo con operacional tiene la ventaja de no necesitar inductores.
El circuito de la figura 3 es un filtro activo de dos polos teniendo por base un amplificador operacional con FET del tipo TL081.

Este circuito es recomendado para aplicaciones que exijan factores Q menores que 10, y ganancia ligeramente mayor que la raíz cuadrada del factor Q. Así, para un factor Q igual a 5 tenemos una ganancia del orden de 2 veces.
Los valores de los componentes para este filtro son calculados a partir de las siguientes fórmulas:
R1 = Q / (2 x π x f x G x C)
R2 = Q / [ (2 x Q2 - G) x 2 x π x f x C ]
R3 = R4 = 2Q / (2 x π x f x C)
Donde:
f : frecuencia central del filtro (Hz)
Q : factor de calidad
G : ganancia
C : capacitancia (F)
Tomemos como ejemplo un filtro con frecuencia central de 800Hz. R2 es un potenciómetro con dos veces el valor calculado que permite ajustar precisamente la frecuencia.
Este valor mayor es sugerido para com pensar las tolerancias de los demás componentes. Para la banda de audio los valores de los capacitores están típicamente en la banda de 10 a 100 nF.
Considerando f = 800 Hz, Q = 5, G = 2 y C = l10 nF, tenemos:
R1 = Q / (2 x π x f x G x C)
R1 = 5 / (6,28) x (800) x (2) x (0,01 x 10-6)
R1 = 49,761 Ω = 50 kΩ
R2 = Q / [ (2 x Q2 - G) x 2 x π x f x C ]
R2 = 5 / (50 - 2) x (6,28) x (800) x (0,01 x 10-6)
R2 = 2073 Ω = 2,2 kΩ
R3 = R4 = 2Q / (2 x π x f x C)
R3 = R4 = 10 / (6,28) x (800) x (0,01 x 10-6)
R3 = R4 = 199,045 Ω = 200 kΩ
En la figura 4 tenemos la curva de respuesta de este filtro. Esta curvar tiene como referencia una tensión de entrada de 4Vpp.

Filtros pasa-altos y pasa-bajos De los muchos tipos de filtros que se pueden usar para dejar pasar señales solamente de altas o solamente de bajas frecuencias, el Butterworth" es el mejor. Filtros complejos normalmente usan redes de primero y segundo orden. Las redes de primer orden no son muy útiles, porque sólo podemos controlar la frecuencia central, mientras que en las de segundo orden podemos, además de la frecuencia central, controlar también la impedancia y la amortiguación o su inverso, el factor Q.
En la figura 5 tenemos una configuración simple de filtro con seguidor de tensión.

En este circuito los capacitores presentan un efecto muy pequeño en las bajas frecuencias, lo que tiene como resultado una respuesta plana en esta región del espectro.
Mientras tanto, en las altas frecuencias los capacitores desvían separadamente la señal hacia puntos de baja impedancia, lo que hace quela respuesta caiga.
Un filtro de dos etapas hace que la respuesta en las altas frecuencias carga con el cuadrado de la frecuencia, de ahí el nombre de filtro de segundo orden para esta configuración.
La respuesta comienza plana en las frecuencias más bajas para caer después com atenuación de 12dB por octava, inicialmente, o 4odB por década, pasando la frecuencia de corte.
Una buena aproximación para el cálculo de este tipo de filtro puede obtenerse con la fijación de R1 igual a R2 y C1 igual a C2. Así, la frecuencia de corte puede ser calculada por:
fo = 1 / (2 . π . R . C)
Tenernos aquí el filtro de " componentes iguales" con una ganancia de 1,586 (+4dB) para una red Butterworth de segundo orden, y esto es lo único que hace que el circuito funcione adecuadamente.
Como el amplificador operacional opera en la configuración no inversora, el resistor de realimentación RB debe ser 0,586 veces el valor del resistor de entrada RA para una ganancia de 1,586.
Para proyectar un filtro pasa-bajos con frecuencia de corte de 1.500 Hz proceda de la siguiente manera:
Fije RA en 47 k,. RB deberá ser entonces R A x 0,586 o aproximadamente 27k. Si fijamos los capacitores en 10 nF los resistores serán seleccionados a partir de la fórmula:
R1 = R2 = 1 / (2 . π . f . C)
R1 = R2 = 1 / (6,28).(1500).(0,01 x 10-6)
R1 = R2 = 10,617 kΩ = 10 kΩ
El simple cambio de posiciones entre los resistores y los capacitores nos lleva al filtro pasa-altas mostrado en la figura 6.

La ganancia y banda pasante son los mismos dela versión anterior.
En la figura 7 damos las curvas de respuesta en frecuencia para las dos versiones.

Filtro pasa-banda con realimentación múltiple
El filtro básico pasa-banda de "feedback" múltiple o realimentación se emplea cuando se desea un factor Q del orden de 15 y una ganancia "moderada".
La única dificultad que se encuentra en la utilización de tales filtros es que a medida que el factor Q aumenta los mismos se vuelven críticos, acentuándose la dificultad para hacer su sintonía.
La experiencia muestra que filtros pasa-bandas activos de alta performance y Q alto no pueden ser proyectados eficientemente con un amplificador operacional único.
Así, las versiones con un único operacional son indicadas para los casos en que se desea bajo factor Q (típicamente entre 2 y 5). Afortunadamente, los valores en esta banda son indicados para muchas aplicaciones en audio tales como ecualizadores, controles de tono, etc.
En la figura 8 tenemos un circuito de una etapa única de realimentación múltiple donde el amplificador operacional se conecta en modo inversor.
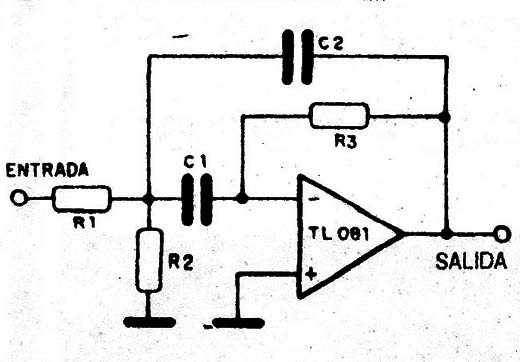
El resistor R3 de la salida a la entrada inversora fija la ganancia y la corriente a través del capacitor Cl, que determina la frecuencia de operación. El capacitor C2 proporciona la realimentación de la salida para la unión de R1 con R2.
C1 y C2 deben ser siempre del mismo valor. El resistor R2 puede ser ajustable para hacer la sintonía.
La frecuencia está dada por la siguiente fórmula:
fo = [ 1 / (2 . π . C) ] . [ (1/R3) . { ( R1 + R2 ) / (R1 . R2) } ]½
Al proyectar un filtro de este tipo se parte de C1 y C2 con valores iguales entre 10 y 100 nF para la banda de audio, 10 que resulta con valores razonables para los resistores.
Vamos a suponer el proyecto de un filtro para 10 kHz con factor Q y una ganancia igual a 2.
Los tres resistores son determinados de la siguiente forma:
R1 = Q / (2 . π . f . C . G) = 2388,5 Ω
R1 = 2,4 kΩ
R2 = Q / [ 2 . π . f . C . (2 . Q2 . G) ] = 298,5 Ω
R2 = 300 Ω
R3 = Q / (π . f . C) = 9554 Ω
R3 = 10 kΩ
En esta fórmula tenemos:
G : ganancia : 2
Q : factor de calidad = 3
C : capacitancia : 10 nF
F = frecuencia central : 10 kHz
Filtros con giradores
Los giradores (gyrators) llevan este nombre por el hecho de que su principio de funcionamiento tiene analogías con los giróscopos mecánicos.
Un girador se puede comportar como un inductor y en un filtro activo esto es importante, pues, como dijimos al comienzo del artículo, los inductores para frecuencias bajas son un impedimento para los proyectos prácticos en vista de su costo y tamaño.
Una inductancia presenta una impedancia de:
ZL = j . 2 . π . f . L
Donde:
ZL: es la impedancia en Ω.
f:es la frecuencia en Hz
L: es la inductancia en henrys
J: es el operador imaginario que equivale a raíz de -1 necesario por el hecho que hay una rotación de fase donde la corriente se adelanta a la tensión.
Para simular una inductancia precisamos de un circuito que satisfaga esta ecuación. En la figura 9 tenemos tal circuito.

Los amplificadores A y B son del tipo "operacionales de transconductancia" que deben ser iguales, excepto por el hecho de que uno de ellos invierte la fase de la serial.
Para efecto de los cálculos, suponiendo G 1 a ganancia, tenemos:
|Gm1| = |Gm2|
Para el circuito específicamente tenemos
IIN = Gm.E1 (I)
ZIN = EIN/IIN (II)
EIN = -IC / Gm (III)
Sustituyendo las ecuaciones I y III en la ecuación II, tenemos:
ZIN = (-IC / Gm) / (Gm . E1)
ZIN = [ 1 / (Gm2 . E1) ] . (-IC / Gm)
ZIN = -IC / (Gm2 . E1) (IV)
Pero, como IC es dado por:
IC = E1 / XC = [ E1 / {1 / (j . 2 . π . f . c )} ]
IC = -j.(2 . π . f . C). E1 (V)
Sustituyendo la ecuación V en la ecuación IV, tenemos:
ZIN = [ { -(-j . 2 . π . f . C) . E1 }/ (Gm2 . E1) ]
ZIN = [ -(-j . 2 . π . f . C) / Gm2 ]
ZIN = (j . 2 . π . f . C) / Gm2 (VI)
La ecuación VI puede ser "mejorada" si hiciéramos:
L = C / Gm2 (VII)
Reordenando la ecuación llegamos entonces a:
ZIN = XL = j . 2 . π . f ( C / Gm2) (VIII)
Esta ecuación corresponde justamente a la de una inductancia, poro sin inductor! Esto muestra que tal circuito puedo ser usado eficientemente para simular un inductor de cualquier valor en un filtro!
REFERENCIAS
OP AMP Cicuits Design and Applications Joseph Carr - TAB 787 - 1976.
Linear and Interface Circuits Applications Texas Instruments - 1985.
Getting Acquainted With the IC - Rufus P. Tuner – Howard Sams – 1975
Art095 - 1989




